
 На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=32, MD=8, H — точка пересечения высот треугольника ABC. Найдите AH.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=32, MD=8, H — точка пересечения высот треугольника ABC. Найдите AH.
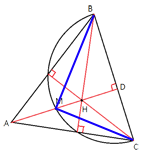 Проведем отрезки CM и MB.
Проведем отрезки CM и MB.
∠BMC является
вписанным в окружность и опирается на дугу в 180° (так как BC - диаметр окружности).
Следовательно, ∠BMC=90° (по
теореме о вписанном угле).
Получается, что треугольник MBC -
прямоугольный.
Рассмотрим треугольники MBC и MBD.
∠BMC=∠BDM=90°
∠MBD - общий.
Следовательно, данные треугольники
подобны (по
первому признаку подобия).
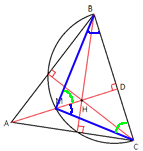 Рассмотрим треугольники MBC и MDС.
Рассмотрим треугольники MBC и MDС.
∠BMC=∠MDC=90°
∠MCD - общий.
Следовательно, данные треугольники
подобны (по
первому признаку подобия).
Значит треугольник MBD подобен треугольнику MDС.
Тогда: MD/BD=CD/MD
MD2=CD*BD
82=CD*BD
64=CD*BD
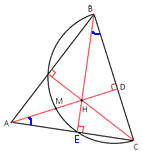 Вернемся к первоначальному рисунку и рассмотрим треугольники AHE и BHD.
Вернемся к первоначальному рисунку и рассмотрим треугольники AHE и BHD.
∠AEH=∠BDH=90°
∠AHE=∠BHD (так как это
вертикальные углы).
Следовательно, используя
теорему о сумме углов треугольника, получаем, что ∠HAE=∠HBD.
Рассмотрим треугольники ADC и BDH.
∠HAE=∠HBD (как мы уже выяснили).
∠ADC=∠BDH=90°
Следовательно, данные треугольники
подобны (по
первому признаку подобия).
Тогда:
AD/BD=DC/DH
AD*DH=BD*DC=64 (см. выше).
DH=64/AD=64/32=2
AH=AD-DH=32-2=30
Ответ: AH=30
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=3 и CH=1. Найдите cosB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=3 и CH=1. Найдите cosB.
 В остроугольном треугольнике ABC высота AH равна 20√
В остроугольном треугольнике ABC высота AH равна 20√
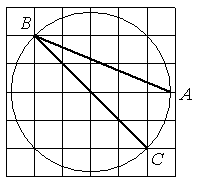 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
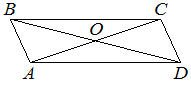 Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=24, BD=28, AB=6. Найдите DO.
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=24, BD=28, AB=6. Найдите DO.
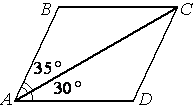 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
Комментарии: