
Задача №20 из 42 |
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
А) 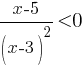
|
1) 
|
Б) 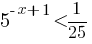
|
2) 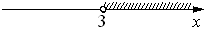
|
| В) (x-3)(x-5)>0 |
3) 
|
| Г) log2(x-3)<1 |
4) 
|
Решим каждое неравенство:
А) 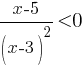
Это неравенство будет меньше нуля, только когда числитель будет меньше нуля, так как знаменатель всегда положителен. Следовательно, данное неравенство можно упростить:
x-5<0 => x<5, подходит вариант 4).
Б) 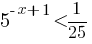
5-x+1<5-2
Применим теорему для решения показательных неравенств:
-x+1<-2 (знак сохраняется так как 5>1)
-x<-3 |*(-1)
x>3 (знак поменялся так как мы домножили на отрицательное число).
Подходит вариант 2).
В) (x-3)(x-5)>0
Найдем корни соответствующего уравнения:
(x-3)(x-5)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x-3=0 => x1=3
2) x-5=0 => x2=5
x2-5x-3x+15>0
x2-8x+15>0

График данной функции - парабола, коэффициент а=1, т.е. положительный, следовательно ветви параболы направлены вверх.
Функция больше нуля, когда ее график располагается выше оси Х. В данном случае на диапазонах (-∞3) и (5;+∞) - подходит вариант 1).
Г) log2(x-3)<1
По второму свойству логарифмов преобразуем правую часть неравенства:
log2(x-3)
По теореме для решения логарифмических неравенств:
 x-3<2
x-3<2
x-3>0
 x<5
x<5
x>3
Подходит вариант 3).
Ответ:
A)
Б)
В)
Г)
4)
2)
1)
3)
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение x2+8=6x.
Если уравнение имеет более одного корня, в ответе укажите больший из них.
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 9 кусков, если по жёлтым — 12 кусков, а если по зелёным — 8 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Каждому из четырёх неравенств в левом столбце соответствует одно
из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| A) 2-x+1<0,5 | 1) (4;+∞) |
| Б) (x-5)2/(x-4)<0 | 2) (2;4) |
| В) log4x>1 | 3) (2;+∞) |
| Г) (x-4)(x-2)<0 | 4) (-∞;4) |
Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны
при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) (x-1)2(x-4)<0 | 1) (-∞; 1)∪(4; +∞) |
Б) 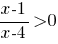 |
2) (1; 4)∪(4; +∞) |
| В) (x-1)(x-4)<0 | 3) (-∞; 1)∪(1; 4) |
Г) 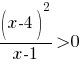 |
4) (1; 4) |
Комментарии: