
Задача №42 из 42 |
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) (x-1)2(x-4)<0 | 1) (-∞; 1)∪(4; +∞) |
Б) 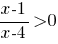 |
2) (1; 4)∪(4; +∞) |
| В) (x-1)(x-4)<0 | 3) (-∞; 1)∪(1; 4) |
Г) 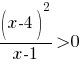 |
4) (1; 4) |
Для начала посмотрим на все неравенства:
Во-первых, они строгие.
Во-вторых, они все представляют из себя либо произведение скобок, либо деление.
Следовательно, мы можем записать Область Допустимых Значений (ОДЗ) для всех неравенств сразу:
x≠1 (так как в неравенствах А),Б) и В) левая часть становится равна нулю, а у нас это невозможно из-за строгости неравенства, либо получается деление на ноль в неравенстве Г)).
x≠4 (по тем же самым причинам).
Теперь решим каждое неравенство:
А) (x-1)2(x-4)<0
Произведение меньше нуля, это возможно только когда один из множителей меньше нуля. (x-1)2 - не может быть меньше нуля, так как квадрат всегда положителен, получается, что надо только решить неравенство:
x-4<0
x<4, т.е. (-∞; 4), но нам надо выколоть значение из ОДЗ (x≠1).
Тогда получаем:
(-∞; 1)∪(1; 4) - это вариант 3).
Б) 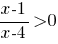
Дробь больше нуля, когда и числитель и знаменатель одновременно или больше нуля или меньше нуля, поэтому рассмотрим два варианта:
a) x-1>0 и x-4>0
x>1 и x>4
Ответ, который подходит для обоих неравенств - x>4 или (4; +∞)
b) x-1<0 и x-4<0
x<1 и x<4
Ответ, который подходит для обоих неравенств - x<1 или (-∞; 1)
Объединяем оба диапазона, получаем:
(-∞; 1)∪(4; +∞) - это решение 1).
В) (x-1)(x-4)<0
Как уже говорилось выше, произведение меньше нуля, когда один из множителей меньше нуля, поэтому опять надо рассмотреть два случая:
a) x-1<0 и x-4>0
x<1 и x>4
Нет такого x, который подходил бы обоим этим неравенствам, т.е. для такого случая решения нет.
b) x-1>0 и x-4<0
x>1 и x<4
Ответ, который подходит для обоих неравенств - 1<x<4 или (1; 4).
Так как в случае а) ответа нет, то (1; 4) и будет решением первоначального неравенства - это решение 4)
Г) 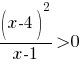
Дробь больше нуля, когда и числитель и знаменатель одновременно или больше нуля или меньше нуля, но так как в числителе стоит квадрат скобки, который всегда положительный, то и знаменатель должен быть положительным:
x-1>0
x>1 или (1; +∞).
Остается только выколоть значение из ОДЗ (x≠4), получаем:
(1; 4)∪(4; +∞) - это решение 2)
Ответ:
| НЕРАВЕНСТВА | А) | Б) | В) | Г) |
| РЕШЕНИЯ | 3) | 1) | 4) | 2) |
Поделитесь решением
Присоединяйтесь к нам...
Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 12 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 70 очков, если известно, что по крайней мере один раз он ошибся?
Найдите корень уравнения 9x+2(1-6x)=-x-6.
Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны
при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
На координатной прямой отмечены точки A, B, C и D.
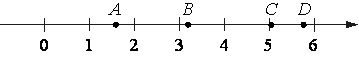
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
| A | 1) √11+√3 |
| B | 2) √11*√3 |
| C | 3) √11-√3 |
| D | 4) (√3)3-2 |
Найдите корень уравнения 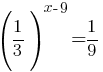
Комментарии: