Задача №34 из 42 |
На координатной прямой отмечены точки A, B, C и D.
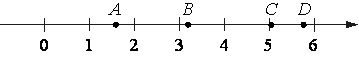
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
| A | 1) √11+√3 |
| B | 2) √11*√3 |
| C | 3) √11-√3 |
| D | 4) (√3)3-2 |
Для начала определим в каких пределах лежат числа √11 и √3.
Для этого возьмем число под корнем и определим для него наименьшие границы, но такие, чтобы легко извлекался корень.
Определить надо довольно точно, поэтому воспользуемся таблицей квадратов.
Визуально перенесем запятую на две цифры влево (т.е. если в таблице число 121, то мы на него смотрим как на 1,21). И ищем число меньше нашего числа под корнем и больше, но максимально приближенное.
Для √11 будет такой порядок действий:
10,89<11<11,56 (в таблице это были числа 1089 и 1156) - теперь извлекаем из всех трех чисел корень.
√10,89<
√11<√11,56
3,3<
√11<3,4
Для √3:
2,89<3<3,24
√2,89<
√3<√3,24
1,7<√3<1,8
А теперь, чтобы найти границы суммы √11+√3 надо попарно сложить границы каждого числа.
1) 3,3+1,7<√11+√3<3,4+1,8
5<√11+√3<5,2
Подходит только число С.
2) 3,3*1,7<√11*√3<3,4*1,8
5,61<√11*√3<6,12
Подходит только число D.
3) 3,3-1,7<√11-√3<3,4-1,8
1,6<√11-√3<1,6
Подходит только A.
4) Этот пункт можно и не вычислять, по остаточному принципу это число B.
| A | B | C | D |
| 3) | 4) | 1) | 2) |
Поделитесь решением
Присоединяйтесь к нам...
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок, делая первый прыжок из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, совершив ровно 8 прыжков?
Решите уравнение x2+10x+21=0.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны
при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?
Найдите корень уравнения √
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: