
Задача №40 из 42 |
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок, делая первый прыжок из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, совершив ровно 8 прыжков?
Во-первых, по условию, кузнечик может прыгать не только в положительную сторону от начала координат, но и в отрицательную - это надо будет учесть.
Во-вторых, так как прыжков 8, а это четное число, то и оказаться (после 8 прыжков) он может только на четных координатах.
Если это не очевидно, то давайте рассмотрим поподробней:
Делая свой первый прыжок, кузнечик оказывается на нечетной координате 1 или -1 (для простоты объяснения предположим, что он прыгнул на 1). Следовательно, вторым прыжком он прыгает на соседние (т.е. четные координаты), на 0 или на 2 и т.д. Т.е. любой нечетный прыжок даст только нечетную координату, а любой четный - только четную.
Так как прыжков только 8, то максимальное расстояние может быть или 8 или -8.
Но так же он может оказаться и на любой четной координате между -8 и 8. Например, кузнечик прыгает на 7 прыжков в положительную сторону и на 1 в отрицательную, при этом он оказывается на 6 и т.д.
Т.е. он может оказаться на -8, -6, -4, -2, 0, 2, 4, 6 и 8 - таких координат 9.
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
Найдите корень уравнения 4x-6=64.
Найдите корень уравнения 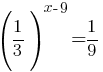
На координатной прямой отмечены точки A, B, C и D.

Число m равно √
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
| A | 1) 2m-5 |
| B | 2) m3 |
| C | 3) m-1 |
| D | 4) -1/m |
На координатной прямой отмечены точки A, B, C и D.

Число m равно √
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА |
| A | 1) 2m-5 |
| B | 2) m3 |
| C | 3) m-1 |
| D | 4) -1/m |
Найдите корень уравнения -5+2x=-3x+6.
Комментарии:
(2022-04-10 11:33:40) юлия: СКОЛЬКО СУЩЕСТВУЕТ РАЗЛИЧНЫХ ТОЧЕК НА КООРДИНАТНОЙ ПРЯМОЙ В КОТОРОЙ КУЗНЕЧИК МОЖЕТ ОКАЗАТЬСЯ СОВЕРШИВ12 ПРЫЖКОВ