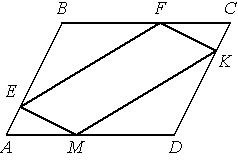
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Рассмотрим треугольники АЕМ и CKF.
АЕ = CK (по условию задачи)
/A=/C (по
свойству параллелограмма)
Т.к. AD=BC (по
свойству параллелограмма), а BF = DM (по условию), то АМ=CF.
Следовательно, треугольники АЕМ и CKF равны (по первому признаку).
Поэтому ЕМ=FK.
Аналогично доказывается, что треугольники EBF и KDM тоже равны, следовательно EF=MK.
Т.е. противоположные стороны данного четырехугольника равны. Соответственно этот четырехугольник - параллелограмм (по
свойству параллелограмма).
Поделитесь решением
Присоединяйтесь к нам...
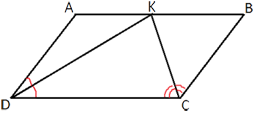Биссектрисы углов C и D параллелограмма ABCD пересекаются в точке K стороны AB. Докажите, что K — середина AB.
Какой угол (в градусах) описывает часовая стрелка за 2 минуты?
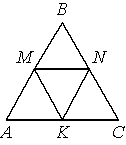В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Сколько досок длиной 3,5 м, шириной 20 см и толщиной 10 мм выйдет из бруса длиной 140 дм, имеющего в сечении прямоугольник размером 50 см × 60 см?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-06-08 11:28:24) Администратор: Света, прямоугольник - это тоже параллелограмм.
(2015-05-26 13:34:16) Света: Но ведь у прямоугольника противолежащие стороны тоже равны.
(2015-05-26 13:33:41) Света: Но ведь у прямоугольника противолежащие стороны тоже равны.
(2015-05-23 20:47:28) Администратор: Малина, а то, что противоположные стороны взаимно равны - доказывает.
(2015-05-23 20:41:29) Малина: То, что треугольники равны, не доказывает, что EFKM параллелограмм