
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
По свойству
равнобедренной трапеции - углы при основании равны.
Тогда ∠ADC=∠BAD=30°+45°=75°.
Сумма углов четырехугольника равна 360°, тогда получаем, что:
360°=75°+75°+∠DCB+∠CBA,
∠DCB+∠CBA=360°-75°-75°=210°, а учитывая, что ∠DCB=∠CBA (по тому
свойству равнобедренной трапеции), получаем ∠DCB=∠CBA=210°/2=105°, эти углы и есть бОльшие в трапеции
Ответ: 105
Поделитесь решением
Присоединяйтесь к нам...
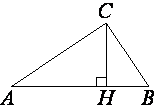 В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
 Сторона ромба равна 8, а расстояние от центра ромба до неё равно 2. Найдите площадь ромба.
Сторона ромба равна 8, а расстояние от центра ромба до неё равно 2. Найдите площадь ромба.
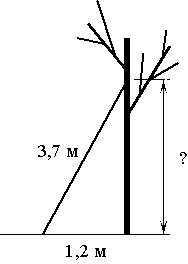 Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
 На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Комментарии: