
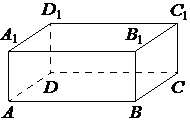
 В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √
Объем параллепипеда равен произведению длины, ширины и высоты.
 Ширина и длина заданы в условии.
Ширина и длина заданы в условии.
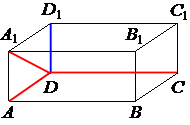
Для удобства, красным цветом выделены известные значения, а синим цветом обозначена сторона, которую необходимо найти.
Для этого рассмотрим треугольник A1AD.
Данный треугольник
прямоугольный, по
опреденению прямоугольного параллелипипеда.
Следовательно, можно применить
теорему Пифагора:
DA12=A1A2+DA2
(√
34=A1A2+9
A1A2=34-9=25
A1A=5
D1D=A1A=5 (так как параллелипипед прямоугольный, т.е. все его грани -
прямоугольники, а противоположные стороны прямоугольника равны по
свойству).
V=D1D*DA*DC=5*3*5=75
Ответ: 75
Поделитесь решением
Присоединяйтесь к нам...
 В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3,
а гипотенуза равна √
В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 3,
а гипотенуза равна √
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
На координатной прямой отмечены точки A, B, C и D.

Число m равно √2.
Установите соответствие между указанными точками и числами в правом столбце, которые им соответствуют.
| ТОЧКИ | ЧИСЛА |
| A | 1) 2m-5 |
| B | 2) m3 |
| C | 3) m-1 |
| D | 4) -1/m |
 Два ребра прямоугольного параллелепипеда равны 8 и 2, а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда.
Два ребра прямоугольного параллелепипеда равны 8 и 2, а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда.
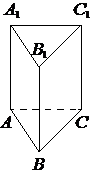 Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.
Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.
Комментарии: