
На координатной прямой отмечены точки A, B, C и D.

Число m равно √2.
Установите соответствие между указанными точками и числами в правом столбце, которые им соответствуют.
| ТОЧКИ | ЧИСЛА |
| A | 1) 2m-5 |
| B | 2) m3 |
| C | 3) m-1 |
| D | 4) -1/m |
Для начала определим в каком диапазоне находится само число m. a<√2<b
Выберем такие a и b, чтобы это было число под корнем, но корень легко извлекался:
√1<√2<√4
Получаем диапазон:
1<√2<2,
т.е. 1<m<2
Теперь проведем преобразования этого неравенства, что получились интересующие нас числа:
1) 2m-5
Возьмем наше неравенство и умножим на 2 все его члены.
1<m<2 |*2
1*2<m*2<2*2
2<2m<4
А теперь вычтем 5 из каждого члена:
2<2m<4 |-5
2-5<2m-5<4-5
-3<2m-5<-1
В диапазоне от -3 до -1 есть только число А.
2) m3
Возведем все члены неравенства в куб:
13<m3<23
1<m3<8
В диапазоне от 1 до 8 находится только число D.
3) m-1
Из всех членов неравенства вычтем 1:
1-1<m-1<2-1
0<m-1<1
Подходит только число C.
4) -1/m
А это число можно даже не вычислять. Методом исключения остается только число B.
Ответ:
| A | B | C | D |
| 1 | 4 | 3 | 2 |
Поделитесь решением
Присоединяйтесь к нам...
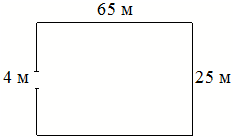 Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.
Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 4 м.
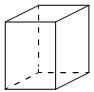 Два ребра прямоугольного параллелепипеда равны 8 и 2, а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда.
Два ребра прямоугольного параллелепипеда равны 8 и 2, а объём параллелепипеда равен 144. Найдите площадь поверхности этого параллелепипеда.
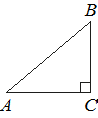 В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.
В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.
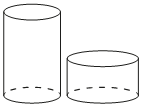 Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
В параллелограмме ABCD диагонали делят его углы пополам и равны 40 и 42. Найдите периметр параллелограмма ABCD.
Комментарии: