
Постройте график функции:
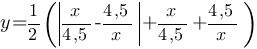 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
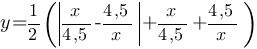
Так как функция содержит модуль, то ее надо разложить на две подфункции:
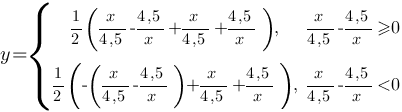
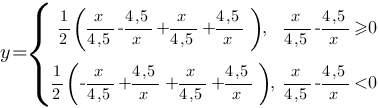

Рассмотрим каждую функцию:
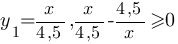
Это означает, что у=x/4,5, когда x/4,5-4,5/x≥0
Найдем этот диапазон.
x/4,5-4,5/x≥0
(x2-4,52)/(4,5x)≥0
Дробь больше нуля в двух случаях:
1) Когда и числитель и знаменатель больше нуля.
2) Когда и числитель и знаменатель меньше нуля.
Рассмотрим первый вариант:
 x2-4,52≥0
x2-4,52≥0
4,5x>0
 x2-4,52≥0
x2-4,52≥0
x>0
 Рассмотрим функцию x2-4,52. Это квадратная функция, следовательно, ее график - парабола. Ветви параболы направлены вверх (так как коэффициент при x2 равен 1, т.е. больше нуля). Очевидно, что корни этой функции равны 4,5 и -4,5. Значение функции будет больше нуля, когда график функции располагается выше оси Х.
Рассмотрим функцию x2-4,52. Это квадратная функция, следовательно, ее график - парабола. Ветви параболы направлены вверх (так как коэффициент при x2 равен 1, т.е. больше нуля). Очевидно, что корни этой функции равны 4,5 и -4,5. Значение функции будет больше нуля, когда график функции располагается выше оси Х.
По общему графику слева видно, функция будет больше нуля на диапазоне (-∞;-4,5)∪[4,5;+∞).
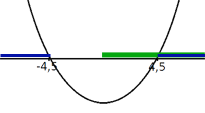 На графике справа синим цветом отмечен диапазон первого неравенства системы, зеленым - второе неравенство. Итоговый диапазон для первого случая - [4,5;+∞)
На графике справа синим цветом отмечен диапазон первого неравенства системы, зеленым - второе неравенство. Итоговый диапазон для первого случая - [4,5;+∞)
Рассмотрим второй случай, когда и числитель и знаменатель меньше нуля.
 x2-4,52<0
x2-4,52<0
4,5x<0
 x2-4,52<0
x2-4,52<0
x<0
По тому же общему графику видно, что функция будет меньше нуля, когда график лежит ниже оси Х.
 На правом графике синим цветом отмечен диапазон первого неравенства системы, зеленым - второе неравенство. Итоговый диапазон для второго случая - (-4,5;0)
На правом графике синим цветом отмечен диапазон первого неравенства системы, зеленым - второе неравенство. Итоговый диапазон для второго случая - (-4,5;0)
Объединяем эти итоговые диапазоны, получаем:
(-4,5;0)∪[4,5;+∞)
Напомним, это диапазон, в котором выражение внутри модуля больше или равно нулю.
Следовательно, выражение внутри модуля меньше нуля на диапазоне (-∞;-4,5]∪(0;4,5), ноль не попадает ни в один из диапазонов, т.к. иначе в функции получится деление на ноль.
Построим график функции 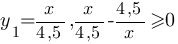 :
:
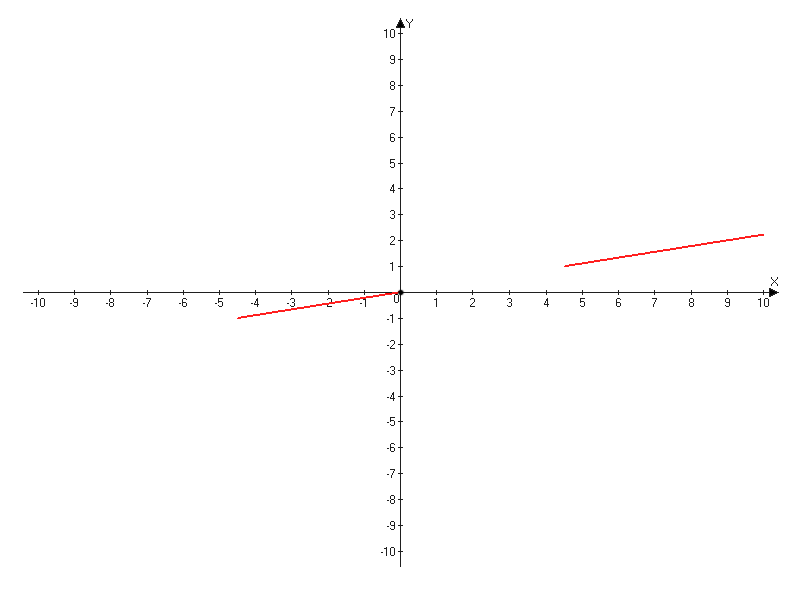
Вторая функция:
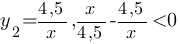 , диапазон мы уже знаем: (-∞;-4,5]∪(0;4,5)
, диапазон мы уже знаем: (-∞;-4,5]∪(0;4,5)
Построим график второй функции:
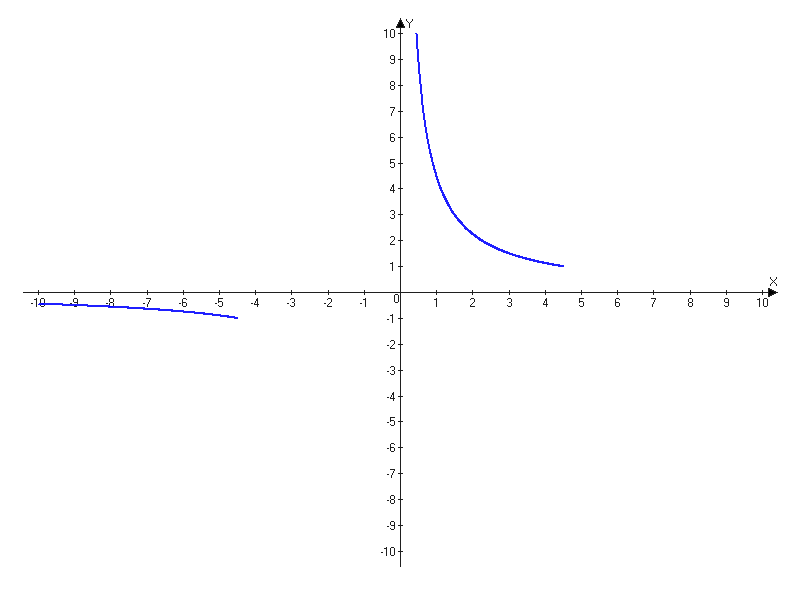
Объединяем графики:
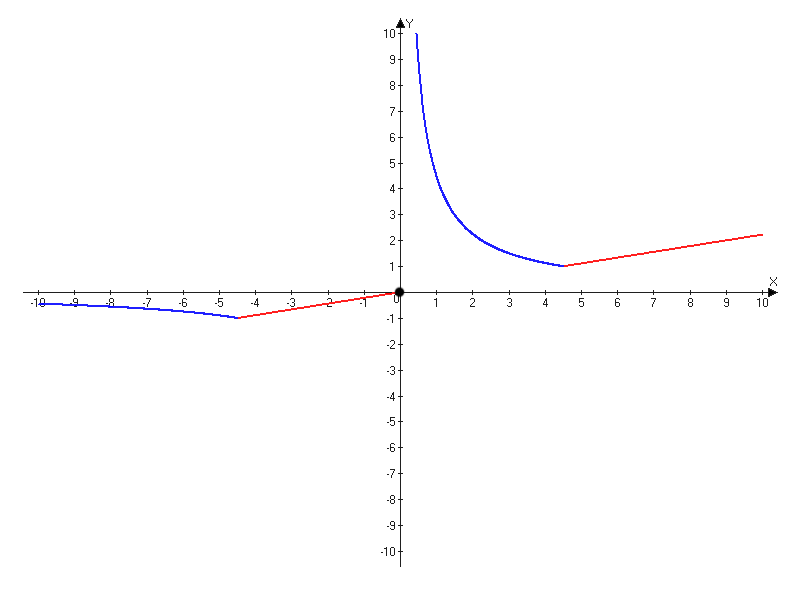
Только одна общая точки будет в двух случаях, в точках "перелома" графика, они отмечены на рисунке. Это точки -4,5 и 4,5.
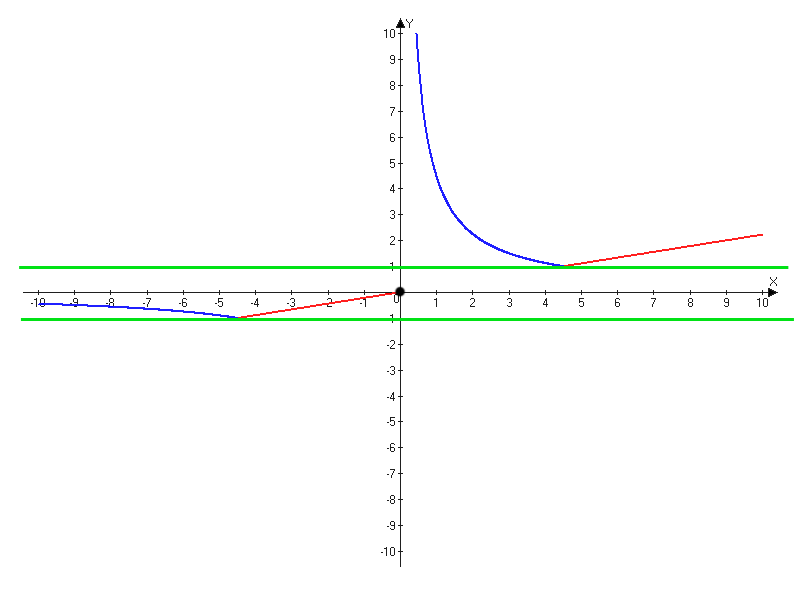
Подставим эти точки в функцию и получим значения m.
m1=y(-4,5)=-1
m2=y(4,5)=1
Ответ: m1=-1 и m2=1
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции:
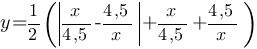 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
А) k<0, b>0 Б) k>0, b<0 В) k<0, b<0 |
1)  |
2)  |
3)  |
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
А) k>0, b<0 Б) k>0, b>0 В) k<0, b>0 |
1)  |
2)  |
3)  |
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) k<0, b<0 2) k<0, b>0 3) k>0, b>0 4) k>0, b<0 |
А)  |
Б)  |
В)  |
Постройте график функции y=x2-4|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Комментарии:
(2017-09-03 21:22:12) Администратор: Нонна, прошу прощения за долгий ответ. Я расписал поподробней решение этих неравенств. Надеюсь, стало понятней, что для неравенства x2-4,5≥0 решением является два диапазона: (-∞;-4,5) и [4,5;+∞).
(2017-09-01 12:35:52) Нонна: Не могу понять: x2-4,52≥0 x>0 Синим цветом отмечен диапазон первого неравенства системы, зеленым - второе неравенство. Итоговый диапазон для первого случая - [4,5;+∞) Почему синим цветом отмечено -∞;4,5. Мне кажется должно быть -4,5;+∞
(2015-04-10 18:33:27) Администратор: Так и есть, просто -(x/4,5-4,5/x)=-x/4,5+4,5/x=4,5/x-x/4,5. Но, тем не менее, я немного расписал решение, чтобы стало понятней.
(2015-04-10 16:27:30) : здесь же модуль стоит и должно быть с минусом и плюс0м