
Установите соответствие между функциями и их графиками.
| ФУНКЦИИ | ГРАФИКИ | |
|
А) y=-x2-x+5 Б) y=(-3/4)x-1 В) y=-12/x |
1) 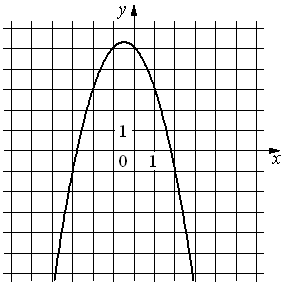 |
2) 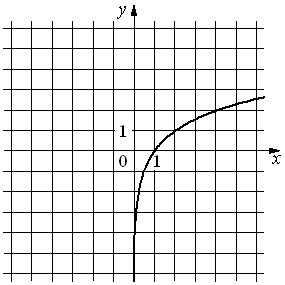 |
3) 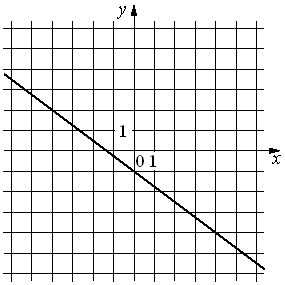 |
4)  |
Рассмотрим функции.
А) y=-x2-x+5 - парабола
Б) y=(-3/4)x-1 - прямая
В) y=-12/x - гипербола
Рассмотрим графики.
1) - Парабола
2) - Заранее неизвестно, но немного похоже на гиперболу или часть параболы.
3) - Прямая
4) - Гипербола
Сразу можно сопоставить прямые: Б) - 3).
Для сопоставления легче всего подставить вместо х какое-либо число, вычислить y и проверить на графике.
Для параболы удобно подставить 0.
А) y=-x2-x+5=-02-0+5=5, смотрим на график, подходит. Значит: А) - 1).
Для гиперболы удобно подставить -2.
В) y=-12/x=-12/(-2)=6, смотрим на график, подходит только для графика 4).
Ответ: А) - 1), Б) - 3), В) - 4)
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=|x|(x+1)-3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции y=x2-5|x|+6. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Большого Шелома?
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Большого Шелома?
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) k>0, b<0 2) k<0, b<0 3) k<0, b>0 4) k>0, b>0 |
А)  |
Б)  |
В)  |
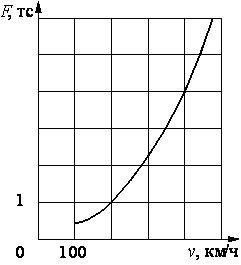 Когда самолёт находится в горизонтальном полёте, подъёмная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолёта. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, на сколько увеличится подъёмная сила (в тоннах силы) при увеличении скорости с 200 км/ч до 400 км/ч.
Когда самолёт находится в горизонтальном полёте, подъёмная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолёта. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, на сколько увеличится подъёмная сила (в тоннах силы) при увеличении скорости с 200 км/ч до 400 км/ч.
Комментарии: