
Постройте график функции y=|x|(x+1)-3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
 y=x(x+1)-3x, при x≥0
y=x(x+1)-3x, при x≥0
y=(-x)(x+1)-3x, при x<0
 y=x2+x-3x, при x≥0
y=x2+x-3x, при x≥0
y=-x2-x-3x, при x<0
 y=x2-2x, при x≥0
y=x2-2x, при x≥0
y=-x2-4x, при x<0
Рассмотрим и построим график для каждой подфункции и объединим их.
1) y=x2-2x, при x≥0
Графиком данной подфункции является парабола. Ветви этой параболы направлены вверх, так как коэффициент при x2 положительный.
Найдем корни уравнения x2-2x=0
x(x-2)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два случая:
1) x1=0
2) x-2=0
x2=2
Построим график по точкам:
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -1 | 0 | 3 |
| X | 0 | -1 | -2 | -3 | -4 |
| Y | 0 | 3 | 4 | 3 | 0 |
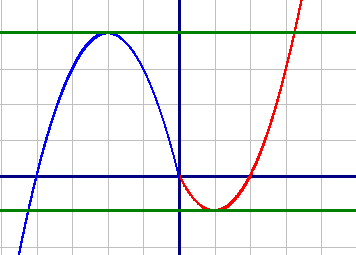 Красный график: y=x2-2x, при x≥0
Красный график: y=x2-2x, при x≥0Поделитесь решением
Присоединяйтесь к нам...
Известно, что графики функций y=x2+p и y=2x-2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Найдите p и постройте график функции y=x2+p, если известно, что прямая y=x имеет с графиком ровно одну общую точку.
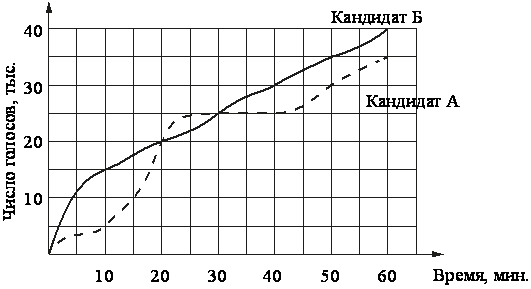 На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 30 минут дебатов?
На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 30 минут дебатов?
Постройте график функции y=x2-4|x|-2x и определите, при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
Постройте график функции 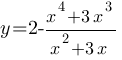 и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Комментарии: