
Постройте график функции y=x2-4|x|-2x и определите, при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
 y=x2-4x-2x, при x≥0
y=x2-4x-2x, при x≥0
y=x2-4(-x)-2x, при x<0
 y=x2-6x, при x≥0
y=x2-6x, при x≥0
y=x2+2x, при x<0
Рассмотрим и построим график для каждой подфункции на определенном им диапазонах и объединим их.
График обеих подфункций - парабола, при чем, ветви параболы направлены вверх (так как коэффициент "а" больше нуля).
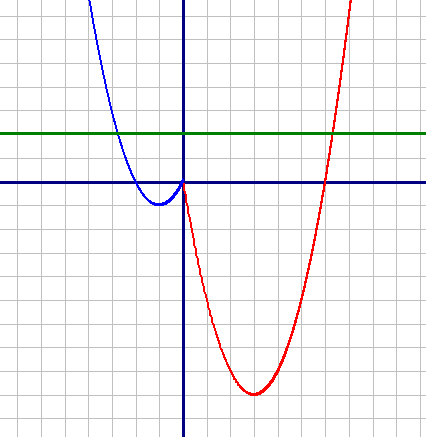 Для первой подфункции (красная):
Для первой подфункции (красная):
| X | 0 | 1 | 3 | 6 |
| Y | 0 | -5 | -9 | 0 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | -1 | 0 | 3 |
Поделитесь решением
Присоединяйтесь к нам...
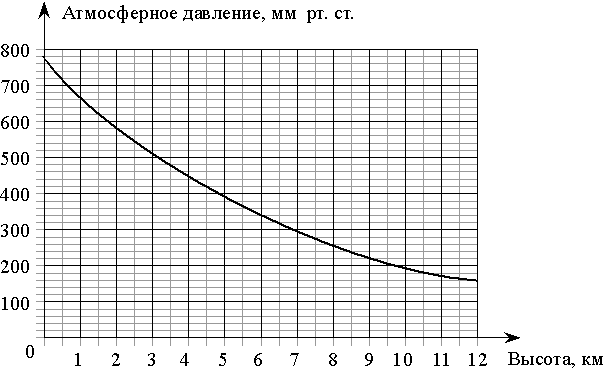
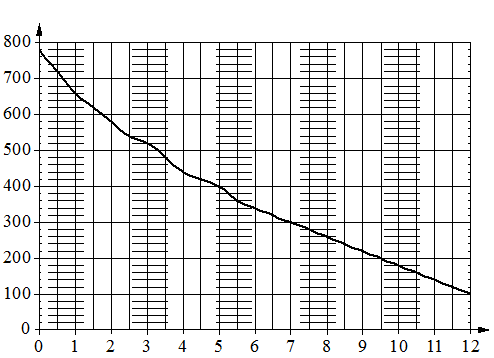 На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление
на высоте 1 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление
на высоте 1 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
Постройте график функции 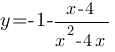 и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Постройте график функции
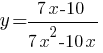 .
.
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 220 миллиметров ртутного столба?
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
А) k<0, b>0 Б) k>0, b<0 В) k<0, b<0 |
1)  |
2)  |
3)  |
Комментарии: