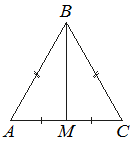В равнобедренном треугольнике ABC медиана BM, проведённая к основанию, равна 12, а tgA=12/5. Найдите длину боковой стороны треугольника ABC.
По
третьему свойству равнобедренного треугольника, BM является не только медианой, но и
высотой.
Следовательно, треугольник ABM -
прямоугольный.
Тогда tgA=BM/AM (по определению tg).
А так как по условию thA=12/5, то:
BM/AM=12/5
12/AM=12/5 |:12
1/AM=1/5
AM=5
AM и BM - катеты треугольника ABM. Необходимо найти AB. Воспользуемся
теоремой Пифагора:
AB2=AM2+BM2
AB2=52+122
AB2=25+144=169
AB=√169=13
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
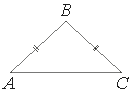В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
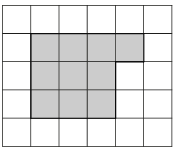План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. Ответ дайте
в квадратных метрах.
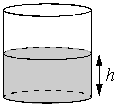Вода в сосуде цилиндрической формы находится на уровне h= 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте
в сантиметрах.
Два ребра прямоугольного параллелепипеда равны 8 и 5,
а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
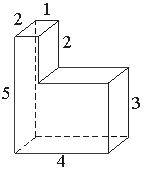Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: