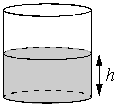
Вода в сосуде цилиндрической формы находится на уровне h= 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте
в сантиметрах.
При переливании воды из одного сосуда в другой, объем воды, естественно, не меняется.
Пусть r - радиус основания первого сосуда.
Тогда площадь основания:
S=πr2
Объем воды:
V=S*h=πr2h
Площадь основания второго сосуда:
S2=πR2=π(2r)2=4πr2 (R - радиус второго сосуда = 2r, по условию)
Объем воды:
V2=S2*h2=4πr2h2
Как мы уже сказали ранее объем воды не меняется, т.е. V=V2, получаем:
πr2h=4πr2h2 |:πr2
h=4h2
80=4h2
h2=80/4=20
Ответ: 20
Поделитесь решением
Присоединяйтесь к нам...
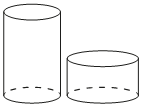Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
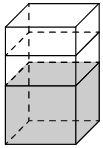В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,8 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
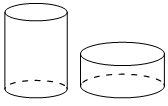Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6,
а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
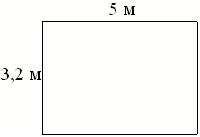На плане указано, что прямоугольная комната имеет площадь 15,7 кв. м. Точные измерения показали, что ширина комнаты равна 3,2 м, а длина 5 м.
На сколько квадратных метров площадь комнаты отличается от значения, указанного на плане?
Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: