
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=x2+4 2) y=-2x+4 3) y=-4/x |
А)  |
Б)  |
В)  |
Рассмотрим формулы.
1) y=x2+4 - парабола
2) y=-2x+4 - прямая
3) y=-4/x - гипербола
Рассмотрим графики.
А) - гипербола
Б) - прямая
В) - парабола
Однозначно можно сопоставить все графики только по виду функции.
Ответ: А) - 3), Б) - 2), В) - 1)
Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
A) 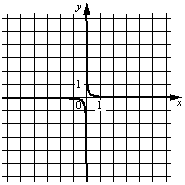 Б)
Б) 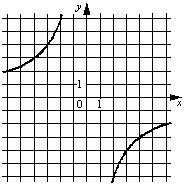 В)
В) 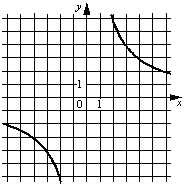
ФОРМУЛЫ
1) y=12/x
2) y=-12/x
3) y=1/(12x)
В таблице под каждой буквой укажите соответствующий номер.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
| А) | 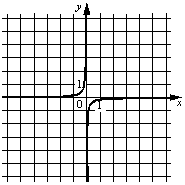 |
Б) | 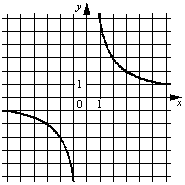 |
В) | 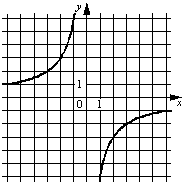 |
ФОРМУЛЫ 1) y=-1/(6x) 2) y=1/(6x) 3) y=-6/x 4) y=6/x |
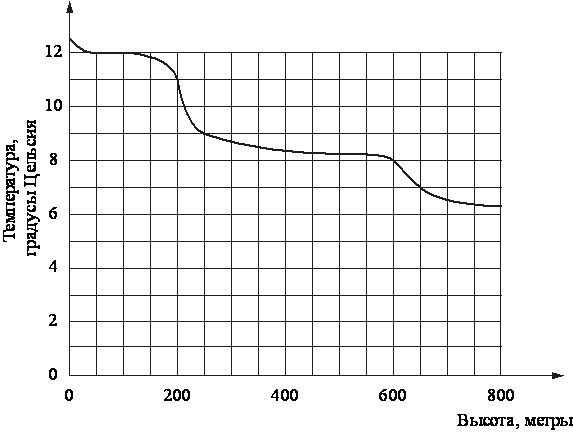 На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря.
На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря.
Определите по графику, на сколько градусов Цельсия температура на высоте 200 метров выше, чем на высоте 650 метров.
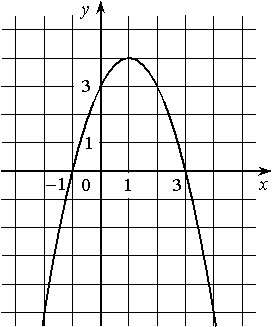 На рисунке изображён график квадратичной функции y=f(x).
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(-1)=f(3)
2) Наибольшее значение функции равно 3
3) f(x)>0 при -1<x<3
Постройте график функции
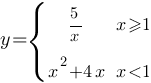 и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Комментарии: