
Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно навстречу ему из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость велосипедиста, если известно, что они встретились в 5 км от пункта А.
Введем обозначения:
vп - скорость перехода
vп+11 - скорость велосипедиста
tп - время в пути перехода
tп-0,5 - время в пути велосипедиста (так как велосипедист сделал получасовую остановку)
Расстояние, которое проехал велосипедист = 13-5=8 км
Расстояние, которое прошел пешеход = 5 км (по условию задачи)
Для пешехода можно составить такое уравнение:
5=vп*tп
Для велосипедиста составим аналогичное уравнение:
8=(vп+11)*(tп-0,5)
8=vпtп-0,5vп+11tп-5,5
Так как 5=vп*tп, то
8=5-0,5vп+11tп-5,5
8,5=11tп-0,5vп
8,5+0,5vп=11tп
tп=(8,5+0,5vп)/11
Подставим полученное tп в уравнение для пешехода:
5=vп*tп=vп*(8,5+0,5vп)/11
55=vп*(8,5+0,5vп)
55=8,5vп+0,5(vп)2
0,5(vп)2+8,5vп-55=0
Найдем дискриминант:
D=(8,5)2-4*0,5*(-55)=72,25+110=182,25
v1=(-8,5+13,5)/(2*0,5)=5
v2=(-8,5-13,5)/(2*0,5)=-22
Так как скорость отрицательной быть не может, значит vп=5 км/ч
Как мы определили ранее скорость велосипедиста = 5+11=16 км/ч.
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение x2-2x+√
Решите неравенство 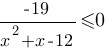
Расходы на одну из статей городского бюджета составляют 6,8%. Выразите эту часть бюджета десятичной дробью.
Решите уравнение x2+3x=10.
Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 3 часа, вернулись обратно через 6 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 9 км/ч?
Комментарии: