
Постройте график функции y=x2-8x-4|x-3|+15 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
В данной функции присутствуем модуль, следовательно функцию надо разложить на две функции, в зависимости от значения модуля:
|x-3|=x-3, при x-3≥0 (т.е. x≥3)
|x-3|=-(x-3), при х-3<0 (т.е. х<3)
Тогда вся функция будет выглядеть так:
 x2-8x-4(x-3)+15, при x≥3
x2-8x-4(x-3)+15, при x≥3
x2-8x-4(-(x-3))+15, при x<3
 x2-8x-4x+12+15, при x≥3
x2-8x-4x+12+15, при x≥3
x2-8x-4(-x+3)+15, при x<3
 x2-12x+27, при x≥3
x2-12x+27, при x≥3
x2-8x+4x-12+15, при x<3
 x2-12x+27, при x≥3
x2-12x+27, при x≥3
x2-4x+3, при x<3
График обеих подфункций - парабола, у обеих подфункций коэффициент "а" равен 1, т.е. больше нуля. Следовательно, ветви обеих парабол направлены вверх.
Построим по точкам графики обеих подфункций, но первый график на диапазоне от 3 до +∞, а второй график на диапазоне от -∞ до 3 (как указано в системе).
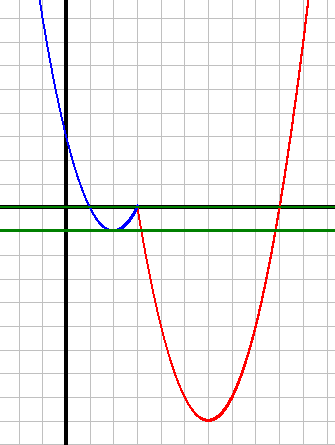 Подфункция y=x2-12x+27 (Красный график)
Подфункция y=x2-12x+27 (Красный график)
| X | 3 | 4 | 5 | 6 | 7 | 8 |
| Y | 0 | -5 | -8 | -9 | -8 | -5 |
| X | 3 | 2 | 1 | 0 | -1 |
| Y | 0 | -1 | 0 | 3 | 8 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=3|x+2|-x2-3x-2 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Постройте график функции
y=x|x|-|x|-3x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
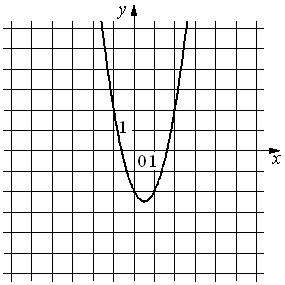 На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке | 1) [2;5] 2) [0;1] 3) [-3;-1] 4) [-2;2] |
Постройте график функции y=x2-8x-4|x-3|+15 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Постройте график функции
y=|x2-x-2|.
Какое наибольшее число общих точек может иметь график данной функции с прямой, параллельной оси абсцисс?
Комментарии:
(2017-04-26 18:55:38) Администратор: Владислав, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-04-26 17:46:17) Владислав: y=x²-4|x|+x Решение