
 На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
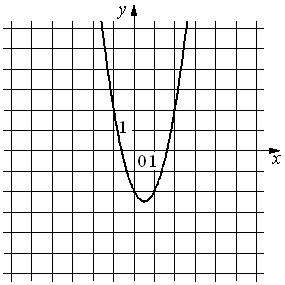
На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке | 1) [2;5] 2) [0;1] 3) [-3;-1] 4) [-2;2] |
Функция возрастает на неком промежутке, если на этом промежутке для любых x1>x2, верно, что y(x1)>y(x2).
И наоборот, функция убывает на неком промежутке, если на этом промежутке для любых x1>x2, верно, что y(x1)<y(x2).
Данная функция возрастает на промежутке [0,5;+∞), следовательно и на промежутке [2;5] тоже возрастает.
Функция убывает на промежутке (-∞;0,5), следовательно и на промежутке [-3;-1] тоже убывает.
Остальные промежутки не подходят.
Ответ: А)-1), Б)-3)
Поделитесь решением
Присоединяйтесь к нам...
 На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. По горизонтали указана высота над уровнем моря
в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 340 миллиметров ртутного столба?
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. По горизонтали указана высота над уровнем моря
в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 340 миллиметров ртутного столба?
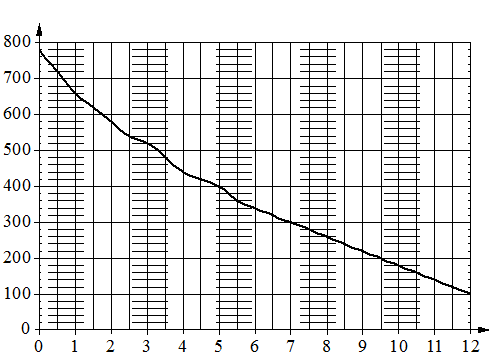 На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление
на высоте 11 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление
на высоте 11 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
 Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Постройте график функции:
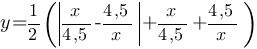 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
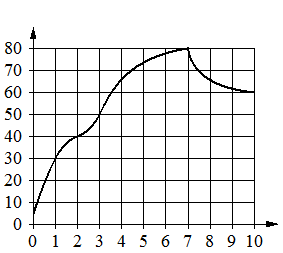 На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику,
через сколько минут с момента запуска двигатель нагреется до 40°C.
На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику,
через сколько минут с момента запуска двигатель нагреется до 40°C.
Комментарии: