
 Какие из следующих утверждений о данной функции неверны? Запишите их номера.
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
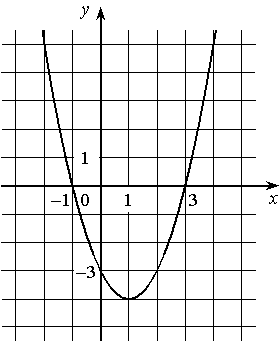
1) Функция убывает на промежутке [1; +∞)
2) Наименьшее значение функции равно -4
3) ƒ(-2)<ƒ(3)
Рассмотрим каждое утверждение:
1) "Функция убывает на промежутке [1; +∞)". Функция убывает, если для любых x1<x2 верно утверждение, что f(x1)>f(x2).
Для примера возьмем x1=2, а x2=3 и посмотрим на график.
f(2)=-3, f(3)=0, т.е. f(2)<f(5), значит функция возрастает. Следовательно, данное утверждение неверно.
2) "Наименьшее значение функции равно -4". Данное утверждение верно, так как по графику видно, что f(1)=-4 и это самая нижняя точка графика.
3) "ƒ(-2)<ƒ(3)". Посмотрим на график:
ƒ(-2)=5
ƒ(3)=0
Т.е. ƒ(-2)>ƒ(3), следовательно данное утверждение неверно.
Ответ: 1) и 3)
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции 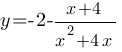 Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Постройте график функции
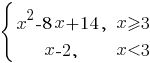
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
A) 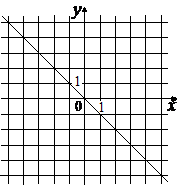 Б)
Б)  В)
В) 
ФОРМУЛЫ
1) y=-x2
2) y=-x
3) y=-1/x
В таблице под каждой буквой укажите соответствующий номер.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=2x+4 2) y=-2x-4 3) y=2x-4 4) y=-2x+4 |
А) 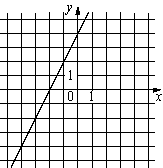 |
Б) 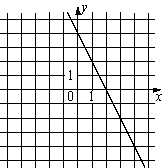 |
В) 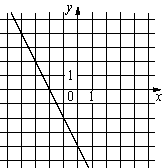 |
Постройте график функции y=x2-5|x|-x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Комментарии: