
Установите соответствие между функциями и их графиками.
| ФУНКЦИИ | ГРАФИКИ | |
|
А) y=3x2+15x+16 Б) y=3x2-15x+16 В) y=-3x2+15x-16 |
1) 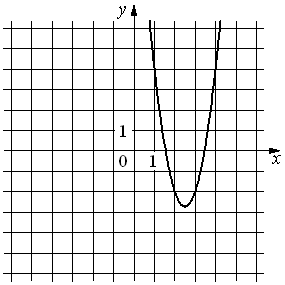 |
2) 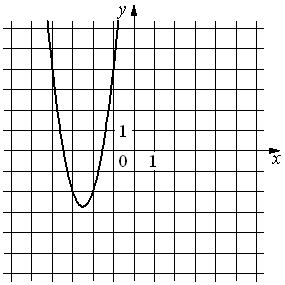 |
3) 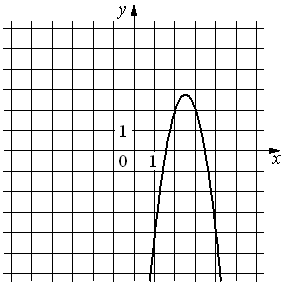 |
Рассмотрим каждую функцию:
А) y=3x2+15x+16
Коэффициент "а" равен 3, т.е. больше нуля, следовательно, ветви параболы направлены вверх. Получается, что может подойти или график 1), или график 2).
Найдем координаты вершины параболы для нашей функции (по формуле x0=-b/(2a)):
x0=-15/(2*3)=-2,5.
Посмотрим на графики, из выбранных нами графиков только у графика 2) координата x0=-2,5, т.е. функции А) соответствует график 2).
Б) y=3x2-15x+16
Коэффициент "а" у этой функции тоже равен 3, т.е. больше нуля, следовательно, ветви параболы тоже направлены вверх.
Найдем координаты вершины параболы:
x0=-b/(2a)=-(-15))/(2*3)=15/6=2,5
То есть подходит только график 1).
В) y=-3x2+15x-16
Коэффициент "а" у этой функции равен -3, т.е. меньше нуля, следовательно, ветви параболы направлены вниз.
Подходит только график 3).
Ответ: А)-2), Б)-1), В)-3).
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
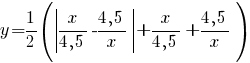
Определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Постройте график функции y=x2+3x-4|x+2|+2 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Постройте график функции y=x2-6|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Постройте график функции y=x2+3x-4|x+2|+2 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Постройте график функции 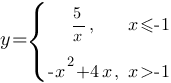 и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
Комментарии: