ОГЭ, Математика. Числовые последовательности: Задача №BA0898 | Ответ-Готов 


Юмор

Автор: Таська
Так выглядит современная программа обучения.
...читать далее

ОГЭ/ГИА

ЕГЭ (базовый уровень)

Числа и вычисления

Алгебраические выражения

Уравнения и неравенства

Числовые последовательности

Функции

Координаты на прямой и плоскости

Геометрия

Статистика и теория вероятностей

Алгебра

Уравнения и неравенства

Функции

Начала математического анализа

Геометрия

Элементы комбинаторики, статистики и теории вероятностей

ОГЭ, Математика.
Числовые последовательности: Задача №BA0898

Задача №162 из 182
Условие задачи:

Геометрическая прогрессия задана условием bn=-480*(1/2)n. Найдите сумму первых её 7 членов.

Решение задачи:

Вариант №1
Чтобы найти сумму первых 7-и членов данной геометрической прогрессии, воспользуемся формулами. В нашем случае, удобней воспользоваться первой. Для этого необходимо узнать b1 - первый член прогрессии и q - знаменатель прогрессии.
b1=-480*(1/2)1=-240 (из условия задачи). А q=1/2.
Тогда:


Ответ: S7=-476,25

Вариант №2
В данной задаче надо найти сумму всего семи первых членов. Поэтому можно просто вычислить значения каждого члена и сложить их:
b1=-480(1/2)1=-480/2=-240
По определению геометрической прогрессии:
b2=b1*q=-240(1/2)=-240/2=-120
b3=b2*q=-120(1/2)=-120/2=-60
b4=-60/2=-30
b5=-30/2=-15
b6=-15/2=-7,5
b7=-7,5/2=-3,75
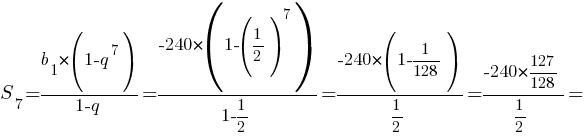
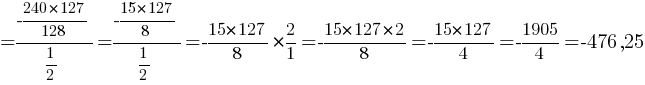
S7=-240-120-60-30-15-7,5-3,75=-476,25
Ответ: -476,25

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела



Задача №9DBAFA

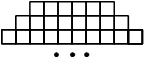Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 2 квадрата больше, чем в предыдущей. Сколько квадратов в 78-й строке?



Задача №589DE9

В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?



Задача №19B940

Дана арифметическая прогрессия (an), в которой a10=-10, a16=-19.
Найдите разность прогрессии.



Задача №414579

Выписаны первые несколько членов арифметической прогрессии: -1; 2; 5; … Найдите сумму первых пятидесяти пяти её членов.



Задача №20B9C2

Дана арифметическая прогрессия (an), разность которой равна 1,6, a1=-1. Найдите a11.

Комментарии:



Найти задачу

По номеру с сайта fipi.ru (шестизначный номер из букв и цифр)
По порядковому номеру в текущем разделе
(от 1 до 182)
По словам
Искать во всех разделах

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки
X

Значение не введено

X

Задайте вопрос по этой задаче.

Ваше имя:


Рейтинг@Mail.ru Copyright otvet-gotov.ru 2014-2021. Все права защищены. Яндекс.Метрика