
Постройте график функции 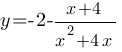 Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Отметим Область допустимых Значений (ОДЗ).
На ноль делить нельзя, следовательно:
x2+4x≠0
x(x+4)≠0
x≠0
x≠-4
Теперь упростим нашу функцию:
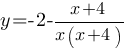
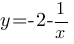
Получили гиперболическую функцию, значит график - гипербола.
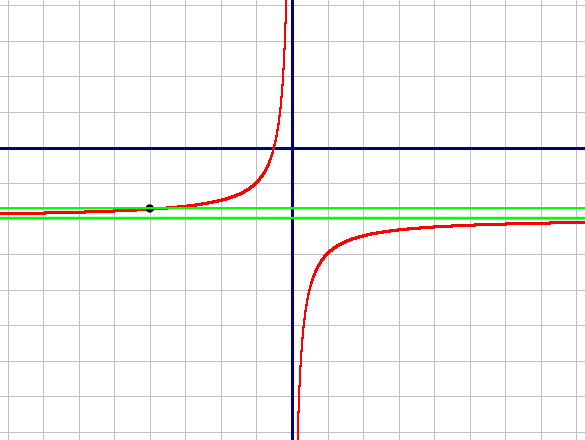 Построим график по точкам:
Построим график по точкам:
| X | -2 | -1 | -0,5 | 0,5 | 1 | 2 |
| Y | -1,5 | -1 | 0 | -4 | -3 | -2,5 |
Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=x2+4 2) y=-2x+4 3) y=-4/x |
А)  |
Б)  |
В)  |
Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=-x2-0,25 ровно одну общую точку. Постройте этот график и все такие прямые.
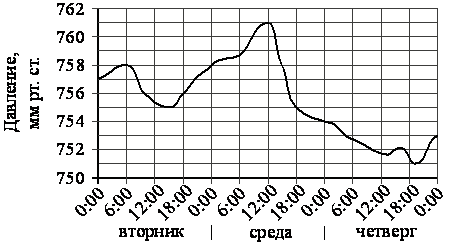 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления во вторник в 18 часов.
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления во вторник в 18 часов.
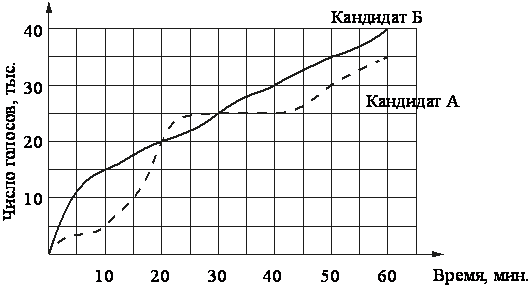 На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 40 минут дебатов?
На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 40 минут дебатов?
Постройте график функции y=x2-|6x+7|.
Определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Комментарии: