Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=x2+4 ровно одну общую точку. Постройте этот график и все такие прямые.
Две функции имеют точку пересечения, это означает, что графики обеих функций имеют общую точку. Следовательно, надо составить систему и решить ее:
y=x2+4
y=kx
kx=x2+4
x2-kx+4=0
Найдем корни этого уравнения:
D=(-k)2-4*1*4=k2-16
В условии сказано, что точка пересечения только одна, следовательно корень уравнения должен быть только один. Это условие выполняется, когда дискриминант равен нулю:
D=k2-16=0
k2-16=0
k2-42=0
(k-4)(k+4)=0
k1=4
k2=-4
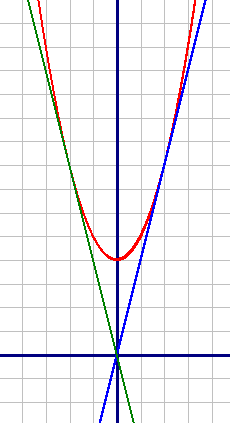Построим графики по точкам:
Получаем функции:
y=x2+4
y=4x
y=-4x
Ответ: k1=4, k2=-4
Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между функциями и их графиками.
| ФУНКЦИИ | ГРАФИКИ | |
|
А) y=3x2+15x+16 Б) y=3x2-15x+16 В) y=-3x2+15x-16 |
1)  |
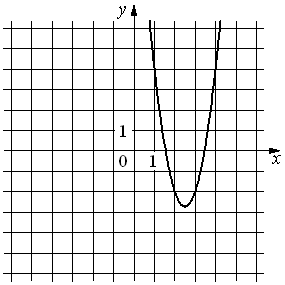2)  |
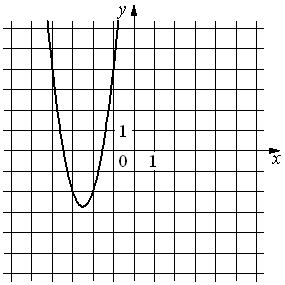3)  |
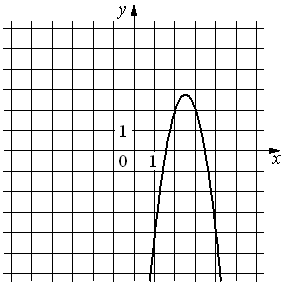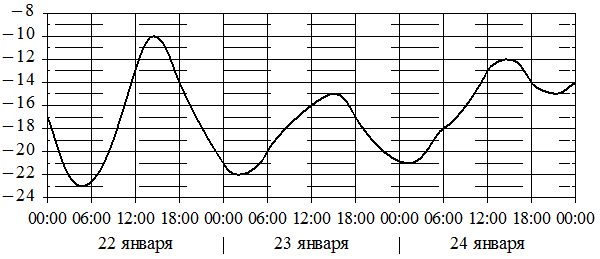На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 24 января. Ответ дайте в градусах Цельсия.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФУНКЦИИ | ГРАФИКИ | ||
|
1) y=-(2/x) 2) y=x2-2 3) y=2x 4) y=2/x |
А)  |
Б)  |
В)  |
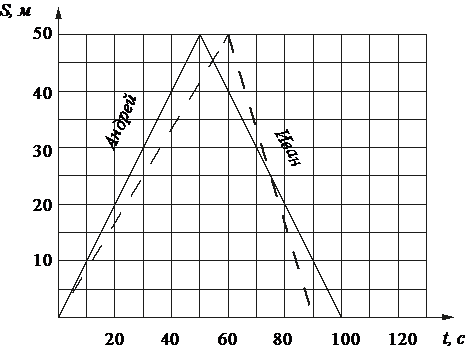Андрей и Иван соревновались в 50-метровом бассейне на дистанции 100 м. Графики их заплывов показаны на рисунке. По горизонтальной оси отложено время, а по вертикальной – расстояние пловца от старта. Кто выиграл соревнование? В ответе запишите, на сколько секунд он обогнал соперника.
Постройте график функции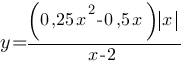 
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: