
Найдите p и постройте график функции y=x2+p, если известно, что прямая y=-2x имеет с графиком ровно одну общую точку.
Две функции имеют точку пересечения, это означает, что графики обеих функций имеют общую точку. Следовательно, надо составить систему и решить ее:
 y=x2+p
y=x2+p
y=-2x
-2x=x2+p
x2+2x+p=0
Найдем корни этого квадратного уравнения:
D=22-4*1*p=4-4p
В условии сказано, что точка пересечения только одна, следовательно корень уравнения должен быть только один. Это условие выполняется, когда дискриминант равен нулю:
D=4-4p=0
p=1
x=-2/(2*1)=-1
y=-2x=-2*(-1)=2
(-1;2) - точка пересечения графиков.
Получаем функцию:
y=x2+1
График функции:
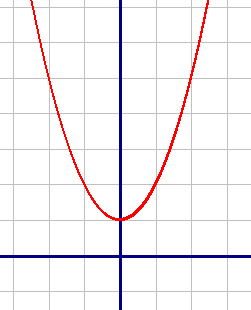
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
 x2, если |x|≤1
x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
Постройте график функции
y=x|x|-|x|-2x.
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции y=x2-6|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=-3 2) y=x-3 3) y=-3x 4) y=3x |
А) 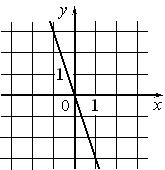 |
Б)  |
В)  |
Постройте график функции 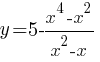 и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Комментарии:
(2015-05-23 19:18:46) Администратор: Саша, да. Приравняли дискриминант к нулю и продолжили решать квадратное уравнение.
(2015-05-23 18:58:26) Саша: То есть мы просто решили квадратное уравнение? Спасибо за ответ!
(2015-05-23 18:51:33) Администратор: Саша, это мы просто вычисляем x в квадратном уравнении по обычной формуле, просто D=0, поэтому его нет...
(2015-05-23 18:47:46) Саша: Здравствуйте! Откуда мы взяли эту часть? x=-2/(2*1)=-1 y=-2x=-2*(-1)=2