Постройте график функции y=|x2-9|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Так как функция содержит
модуль, то данную функцию надо разложить на две функции, в зависимости от значения модуля.
y=x2-9, при x2-9≥0
y=-(x2-9), при x2-9<0
Вычислим при каких значениях х функция меняет свой знак, для этого решим неравенство:
x2-9≥0
Найдем корни уравнения x2-9=0
x2-32=0
Воспользуемся формулой
разность квадратов:
(x-3)(x+3)=0
x1=3
x2=-3
Функция y=x2-9 будет больше нуля в диапазонах, где ее график располагается выше оси Х, и, соответственно, меньше нуля на диапазонах, когда график ниже оси Х.
Итак:
x2-9≥0, когда x∈(-∞; -3]∪[3; +∞)
x2-9<0, когда x∈(-3;3)
Значит можем переписать систему:
y=x2-9, при x ∈ (-∞; -3]∪[3; +∞)
y=-(x2-9), при x ∈ (-3; 3)
y=x2-9, при x ∈ (-∞; -3]∪[3; +∞)
y=-x2+9, при x ∈ (-3; 3)
График каждой из подфункция - парабола, но у первой параболы ветви направлены вверх (так как "а" положительный), а у второй - вниз (так как "а" отрицательный).
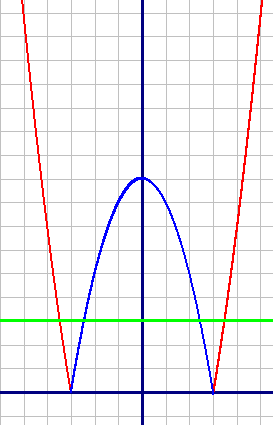Построим оба графика по точкам:
1)y=x2-9, при x ∈ (-∞; -3]∪[3; +∞) (красный график):
| X | -3 | -4 | -5 | 3 | 4 | 5 |
| Y | 0 | 7 | 16 | 0 | 7 | 16 |
| X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| Y | 0 | 5 | 8 | 9 | 8 | 5 | 0 |
Поделитесь решением
Присоединяйтесь к нам...
На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 30 минут дебатов?
Постройте график функции y=2x+6|x|-x2 и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Постройте график функции y=x2-5|x|-x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) k<0, b>0 2) k<0, b<0 3) k>0, b<0 4) k>0, b>0 |
А)  |
Б)  |
В)  |
На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. По горизонтали указана высота над уровнем моря
в километрах, по вертикали — атмосферное давление в миллиметрах ртутного столба. На какой высоте (в км) летит воздушный шар, если барометр, находящийся в корзине шара, показывает давление 340 миллиметров ртутного столба?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: