
Постройте график функции
 x2, если |x|≤1
x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
Чтобы построить график функции состоящей из двух подфункций, необходимо построить график каждой подфункции на указанных для них диапазонах и объединить эти графики.
Так как в данном примере диапазоны обозначены неравенствами с
функцией модуля, то сначала решим эти неравенства:
Функция |x| всегда принимает положительные значения, и |x| будет меньше или равен 1, когда -1≤х≤1, т.е. x⊂[-1;1].
Следовательно |x|>1 на всем остальном пространстве, т.е. x⊂(-∞;-1)∪(1;+∞).
Запишем получившуюся функцию:
 x2, если x⊂[-1;1]
x2, если x⊂[-1;1]
1/x, если x⊂(-∞;-1)∪(1;+∞)
Построим по точкам график обоих подфункций в указанных диапазонах:
x2, если x⊂[-1;1]
| X | -1 | 0 | 1 |
| Y | 1 | 0 | 1 |
| X | -5 | -2 | -1 | 1 | 2 | 5 |
| Y | -0,2 | -0,5 | -1 | 1 | 0,5 | 0,2 |
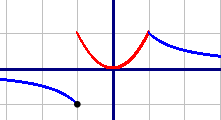 График первой подфункции начерчен красным цветом, график второй подфункции - синим.
График первой подфункции начерчен красным цветом, график второй подфункции - синим.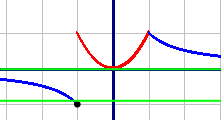 Обратите внимание, что при с=0 прямая касается графика красной подфункции, а при всех остальных значениях - пересекает синюю подфункцию.
Обратите внимание, что при с=0 прямая касается графика красной подфункции, а при всех остальных значениях - пересекает синюю подфункцию.Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=-2 2) y=x-2 3) y=-2x |
А) 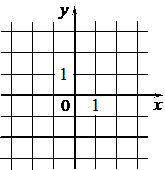 |
Б) 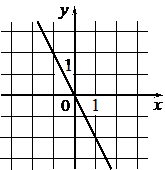 |
В) 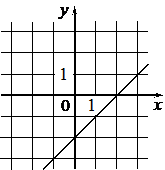 |
На рисунке изображены графики функций вида y=ax2+c. Установите соответствие между графиками и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | |||
|
1) a>0, c<0 2) a<0, c>0 3) a>0, c>0 4) a<0, c<0 |
А) 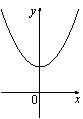 |
Б) 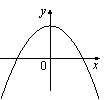 |
В) 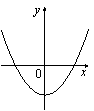 |
Г) 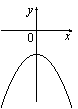 |
 При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1 В до 0,8 В.
При работе фонарика батарейка постепенно разряжается и напряжение
в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1 В до 0,8 В.
Постройте график функции y=|x|x+|x|-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
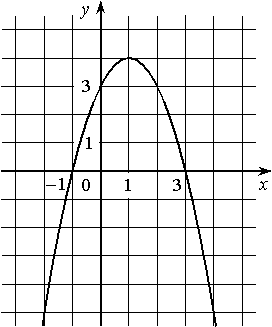 На рисунке изображён график квадратичной функции y=ƒ(x).
На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) ƒ(x)<0 при x<1
2) Наибольшее значение функции равно 3
3) ƒ(0)>ƒ(4)
Комментарии: