
Постройте график функции y=x2+11x-4|x+6|+30 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
В данной функции присутствуем модуль, следовательно функцию надо разложить на две функции, в зависимости от значения модуля:
|x+6|=x+6, при x+6≥0 (т.е. x≥-6)
|x+6|=-(x+6), при х+6<0 (т.е. х<-6)
Тогда вся функция будет выглядеть так:
 x2+11x-4(x+6)+30, при x≥-6
x2+11x-4(x+6)+30, при x≥-6
x2+11x-4(-(x+6))+30, при x<-6
 x2+11x-4(x+6)+30, при x≥-6
x2+11x-4(x+6)+30, при x≥-6
x2+11x+4(x+6)+30, при x<-6
 x2+11x-4x-24+30, при x≥-6
x2+11x-4x-24+30, при x≥-6
x2+11x+4x+24+30, при x<-6
 x2+7x+6, при x≥-6
x2+7x+6, при x≥-6
x2+15x+54, при x<-6
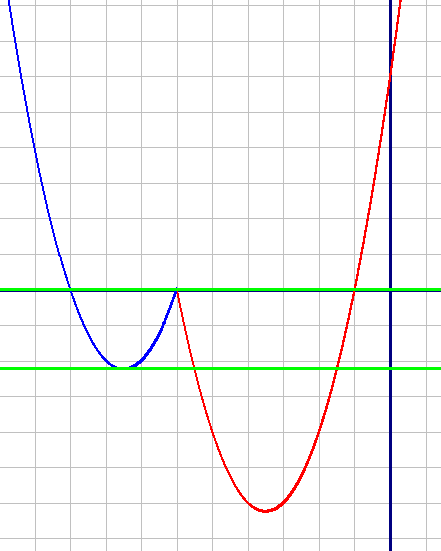 График обеих подфункций - парабола, у обеих подфункций коэффициент "а" равен 1, т.е. больше нуля. Следовательно, ветви обеих парабол направлены вверх.
График обеих подфункций - парабола, у обеих подфункций коэффициент "а" равен 1, т.е. больше нуля. Следовательно, ветви обеих парабол направлены вверх.
Построим по точкам графики обеих подфункций, но первый график на диапазоне от -6 до +∞, а второй график на диапазоне от -∞ до -6 (как указано в системе).
Подункция y=x2+7x+6 (Красный график)
| X | -6 | -5 | -4 | -3 | -2 | -1 | 0 |
| Y | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
| X | -6 | -7 | -8 | -9 | -10 |
| Y | 0 | -2 | -2 | 0 | 4 |
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции
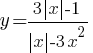
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
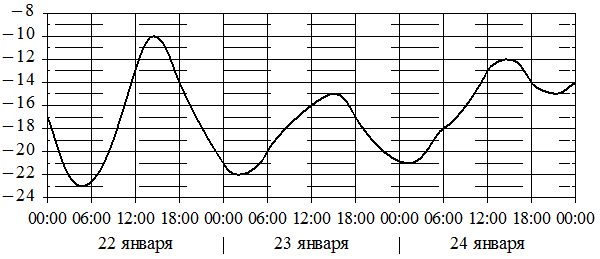 На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 24 января. Ответ дайте в градусах Цельсия.
На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 24 января. Ответ дайте в градусах Цельсия.
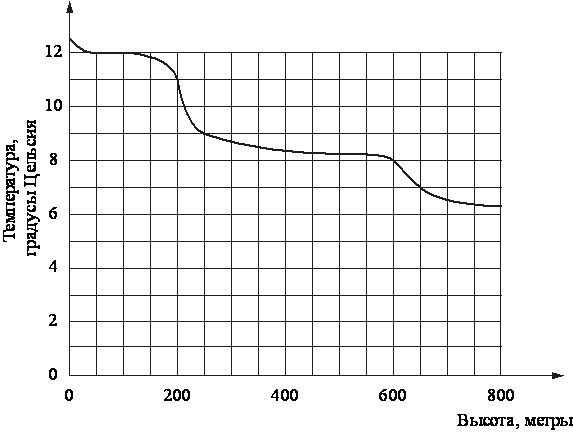 На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря.
На рисунке изображена зависимость температуры (в градусах Цельсия) от высоты (в метрах) над уровнем моря.
Определите по графику, на сколько градусов Цельсия температура на высоте 200 метров выше, чем на высоте 650 метров.
На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) a<0, c<0 2) a>0, c>0 3) a>0, c<0 4) a<0, c>0 |
А)  |
Б)  |
В)  |
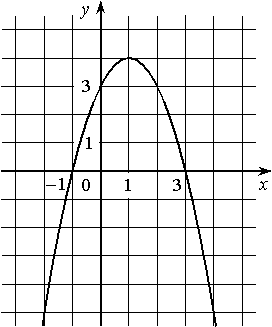 На рисунке изображён график квадратичной функции y=ƒ(x).
На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) ƒ(x)<0 при x<1
2) Наибольшее значение функции равно 3
3) ƒ(0)>ƒ(4)
Комментарии:
(2020-03-11 20:38:08) Администратор: Кто-то, как тут все написано...
(2020-03-08 15:13:55) кто-то: Как тут?