
На координатной прямой отмечены числа а и с.
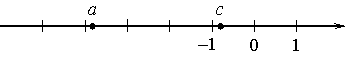
Какое из следующих утверждений неверно?
1) c-a<0
2) ac>0
3) 0<c+1<1
4) -a>0
Рассмотрим числа а и с.
а - отрицательное число, причем -4<a<-3
с - тоже отрицательное число, причем -1<с<0
Рассмотрим каждое утверждение:
1) c-a<0, перенесем "а" в правую часть неравенства.
c<a - т.е. получается, что с меньше а, а это неверно судя ко координатной прямой.
Данное утверждение неверно.
2) ac>0, отрицательное число умноженное на отрицательное всегда в результате даст положительное число, т.е. данное утверждение верно
3) 0<c+1<1
Мы знаем, что -1<с<0, прибавим 1 ко всем числам:
-1+1<с+1<0+1
0<c+1<1, т.е. данное утверждение верно
4) -a>0
Мы знаем, что -4<a<-3, домножим все числа на -1 (при этом не забудем, что знак неравенства меняется на противоположный):
-4*(-1)<a*(-1)<-3*(-1)
4>-a>3
Нас интересует только вторая часть неравенства: -a>3, тогда, естественно, -а>0, т.е. данное утверждение верно
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
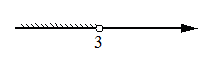
Укажите решение системы неравенств
 x>-1
x>-1
3-x>0
1) 
2) 
3) система не имеет решений
4) 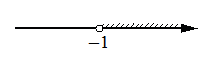
На каком из рисунков изображено решение неравенства x2<9?
1) 
2) 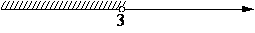
3) 
4) 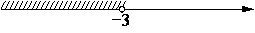
Решение какого из данных неравенств изображено на рисунке?

1) x2-x<0
2) x2-1<0
3) x2-1>0
4) x2-x>0
На каком рисунке изображено множество решений системы неравенств
 -35+5x>0,
-35+5x>0,
6-3x>-18?
1) 
2) 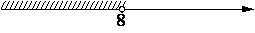
3) система не имеет решений
4) 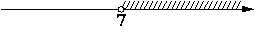
При каком значении р прямая y=x+p имеет с параболой y=x2-3x ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении p.
Комментарии: