Постройте график функции y=|x|(x-1)-3x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
y=x(x-1)-3x, при x≥0
y=(-x)(x-1)-3x, при x<0
y=x2-x-3x, при x≥0
y=-x2+x-3x, при x<0
y=x2-4x, при x≥0
y=-x2-2x, при x<0
Рассмотрим и построим график для каждой подфункции и объединим их.
1) y=x2-4x, при x≥0
Графиком данной подфункции является парабола. Ветви этой параболы направлены вверх, так как коэффициент при x2 положительный.
Найдем корни уравнения x2-4x=0
x(x-4)=0
x1=0
x-4=0
x2=4
Построим график по точкам:
| X | 0 | 1 | 2 | 3 | 4 |
| Y | 0 | -3 | -4 | -3 | 0 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 1 | 0 | -3 |
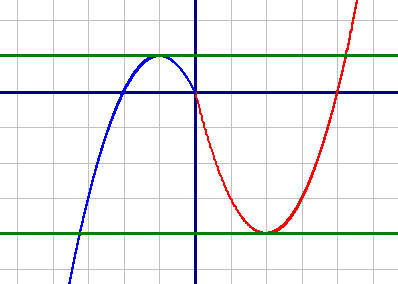Красный график: y=x2-4x, при x≥0Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
А) 
Б) 
В) 
ФОРМУЛЫ
1) y=-(2/x) 2) y=x2-2
3) y=2x
В таблице под каждой буквой укажите соответствующий номер.
Постройте график функции y=|x2-9|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
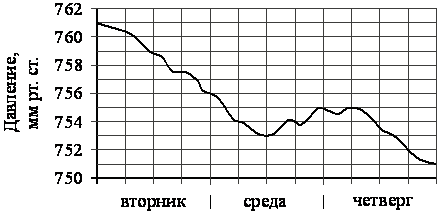На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наибольшее значение атмосферного давления в среду (мм рт. ст.).
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
КОЭФФИЦИЕНТЫ
А) k<0, b<0
Б) k<0, b>0
В) k>0, b<0
ГРАФИКИ
1) 
2) 
3) 
В таблице под каждой буквой укажите соответствующий номер.
Постройте график функции y=x2-3|x|-x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: