
Задача №37 из 42 |
В корзине лежит 40 грибов: рыжики и грузди. Известно, что среди любых 17 грибов имеется хотя бы один рыжик, а среди любых 25 грибов хотя бы один груздь. Сколько рыжиков в корзине?
В данной задаче все просто.
"среди любых 17 грибов имеется хотя бы один рыжик", т.е. возможный максимум груздей = 17-1=16.
"среди любых 25 грибов хотя бы один груздь", т.е. возможный максимум рыжиков = 25-1=24.
Проверяем, что сумма максимумов не превышает общее число грибов:
16+24=40 - полностью удовлетворяет условиям задачи.
Ответ: 24
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение x2=9.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Найдите корень уравнения log3(2x-5)=2.
Найдите корень уравнения log3(2x-5)=2.
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ |
| А) (x-1)2(x-4)<0 | 1) (-∞; 1)∪(4; +∞) |
Б) 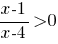 |
2) (1; 4)∪(4; +∞) |
| В) (x-1)(x-4)<0 | 3) (-∞; 1)∪(1; 4) |
Г) 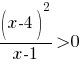 |
4) (1; 4) |
Комментарии: