Решение какого из данных неравенств изображено на рисунке?
1) x2+1<0
2) x2-1<0
3) x2-1>0
4) x2+1>0
Посмотрим на предложенные неравенства:
- все они квадратичные, т.е. графики этих функций - параболы
- у всех аргумент "а" равен еденице, т.е. больше нуля, следовательно ветви их парабол направлены вверх
- графики парабол 1) и 4) будут совпадать, т.к. это одинаковые функции.
- графики парабол 2) и 3) будут совпадать, т.к. это одинаковые функции.
Посмотрим на рисунок решения неравенства:
- корни квадратичной функции должны быть -1 и 1.
Решим уравнение x2+1=0
x2=-1
Данное уравнение не имеет корней, так как ни какое число в квадрате не будет отрицательным. Следовательно неравенства 1) и 4) не подходят.
Решим уравнение x2-1=0
x2-12=0
(x-1)(x+1)=0
x-1=0 => x1=1
x+1=0 => x2=-1
Посмотрим на рисунок, в условии показаны диапазоны, когда график функции выше оси Х, т.е. больше нуля, следовательно, подходит неравенство x2-1>0
Ответ: 3)
Поделитесь решением
Присоединяйтесь к нам...
На координатной прямой отмечено число a.
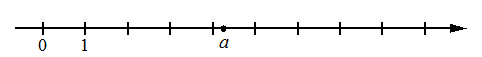
Какое из утверждений для этого числа является верным?
1) 4-a>0
2) 4-a<0
3) a-3<0
4) a-6>0
На координатной прямой отмечены числа a, b и c.
Какая из разностей a-b, a-c, c-b положительна?
1) a-b
2) a-c
3) c-b
4) ни одна из них
Решение какого из данных неравенств изображено на рисунке?
1) x2+1<0
2) x2-1<0
3) x2-1>0
4) x2+1>0
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ |
|
А) k>0, b>0 Б) k>0, b<0 В) k<0, b>0 |
1)  |
2)  |
3)  |
Одно из чисел √40, √46, √53, √58 отмечено на прямой точкой A.
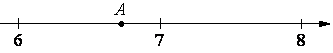
Какое это число?
1) √40
2) √46
3) √53
4) √58
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: