
На координатной прямой отмечено число a.
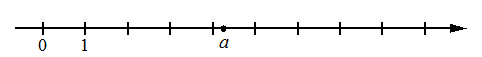
Какое из утверждений для этого числа является верным?
1) 4-a>0
2) 4-a<0
3) a-3<0
4) a-6>0
Для начала отметим, что:
4<a<5
Теперь будем приводить это неравенство к предложенным вариантам.
1) 4-a>0
Начнем преобразовывать наше неравенство:
4<a<5 |*(-1), при умножении на отрицательное число, знаки меняются на противоположные:
-4>-a>-5 |+4
4-4>4-a>4-5
0>4-a>-1
Смотрим на первую часть неравенства:
0>4-a или 4-a<0
Полученное неравенство противоречит первому варианту, т.е. 4-a>0 - НЕВЕРНО.
2) 4-a<0
В пункте 1) мы доказали, что это утверждение ВЕРНО.
3) a-3<0
Опять начнем преобразования нашего неравенства:
4<a<5 |-3
4-3<a-3<5-3
1<a-3<2
Получили, что a-3 больше 1, т.е. никак не может быть меньше нуля. Следовательно, это утверждение НЕВЕРНО.
4) a-6>0
Действуем аналогично:
4<a<5 |-6
4-6<a-6<5-6
-2<a-6<-1
Получили, что a-6 меньше -1, т.е. никак не может быть больше нуля. Следовательно, это утверждение НЕВЕРНО.
Ответ: 2)
Поделитесь решением
Присоединяйтесь к нам...
На координатной прямой отмечено число a.
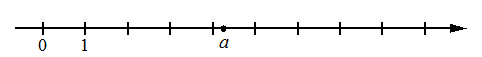
Какое из утверждений для этого числа является верным?
1) 4-a>0
2) 4-a<0
3) a-3<0
4) a-6>0
Постройте график функции 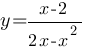 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решите систему неравенств 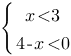
На каком рисунке изображено множество её решений?
1) 
2) Система не имеет решений
3) 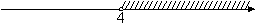
4) 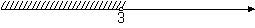
Одна из точек, отмеченных на координатной прямой, соответствует числу 4/5. Какая это точка?

1) A
2) B
3) C
4) D
Решение какого из данных неравенств изображено на рисунке?

1) x2-36≤0
2) x2+36≤0
3) x2-36≥0
4) x2+36≥0
Комментарии: