Автор: ТаськаНа координатной прямой отмечено число a.
Какое из утверждений относительно этого числа является верным?
1) a-5<0
2) 5-a<0
3) a-7>0
4) 6-a>0
Заметим, что 6<a<7
1) Вычтем 5 из всех трех чисел:
6-5<a-5<7-5
1<a-5<2
Следовательно, утверждение 1) неверно.
2) Домножим все три числа на "-1" (не забываем, что знак неравенства поменяется на противоположный).
6*(-1)>a*(-1)>7*(-1)
-6>-a>-7, прибавим 5
-6+5>-a+5>-7+5
-1>5-a>-2
Следовательно, утверждение 2) верно.
3) Вычтем 7 из всех трех чисел:
6-7<a-7<7-7
-1<a-7<0
Следовательно, утверждение 3) неверно.
4) Домножим все три числа на "-1" (не забываем, что знак неравенства поменяется на противоположный).
6*(-1)>a*(-1)>7*(-1)
-6>-a>-7, прибавим 6
-6+6>-a+6>-7+6
0>6-a>-1
Следовательно, утверждение 4) неверно.
Ответ: 2)
Поделитесь решением
Присоединяйтесь к нам...
Какое из данных ниже чисел принадлежит отрезку [7; 8]?
1) 69/11
2) 80/11
3) 90/11
4) 92/11
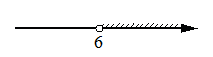
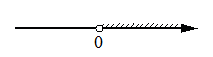
Укажите решение системы неравенств
1) 
2) 
3) 
4) система не имеет решений
Постройте график функции 
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
КОЭФФИЦИЕНТЫ
А) k<0, b>0
Б) k>0, b<0
В) k<0, b<0
1)
2)
3)
Одна из точек, отмеченных на координатной прямой, соответствует числу 5/7. Какая это точка?
1) A
2) B
3) C
4) D
Хочу получать новые решения
Ни какого спама
Комментарии: