
Постройте график функции
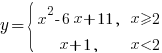
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Чтобы построить график этой функции, надо построить график каждой подфункции на указанных для подфункций диапазонах.
y1=x2-6x+11 на диапазоне [2;+∞)
y2=x+1 на диапазоне (-∞;2)
Проанализируем графики.
Первая подфункция:
1) график - парабола
2) так как коэффициент а=1 (т.е. больше нуля), то ветви направлены вверх
3) Найдем корни соответствующего уравнения через
дискриминант x2-6x+11=0, чтобы узнать в каких точках парабола пересекает ось Х:
D=(-6)2-4*1*11=36-44=-8
D<0, это означает, уравнение не имеет корней, а значит парабола не пересекает ось Х.
Дальше будем строить по точкам (красный график):
| X | 2 | 3 | 4 | 5 |
| Y | 3 | 2 | 3 | 6 |
| X | 2 | 1 | 0 |
| Y | 3 | 2 | 1 |
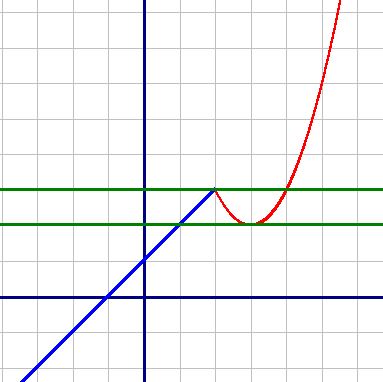 y=m - это прямые, параллельные оси Х. Зеленым цветом построены прямые y=m. Очевидно, что только две прямые будут иметь только 2 общие точки с нашим графиком - это прямая, проходящая через точку "излома" графика, и прямая, касающаяся вершины параболы.
y=m - это прямые, параллельные оси Х. Зеленым цветом построены прямые y=m. Очевидно, что только две прямые будут иметь только 2 общие точки с нашим графиком - это прямая, проходящая через точку "излома" графика, и прямая, касающаяся вершины параболы.Поделитесь решением
Присоединяйтесь к нам...
Установите соответствие между функциями и их графиками.
| ФУНКЦИИ | ГРАФИКИ | |
|
А) y=3x2+15x+16 Б) y=3x2-15x+16 В) y=-3x2+15x-16 |
1) 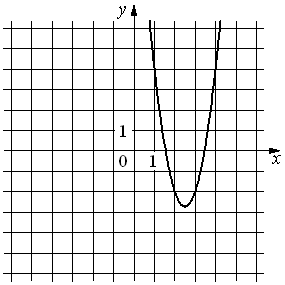 |
2) 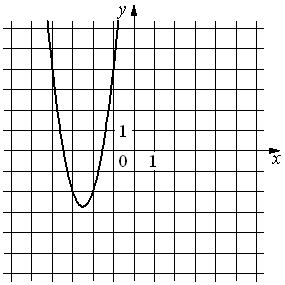 |
3) 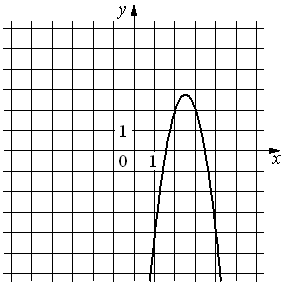 |
Постройте график функции y=|x|(x-1)-3x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции 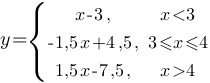 и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции
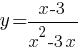
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
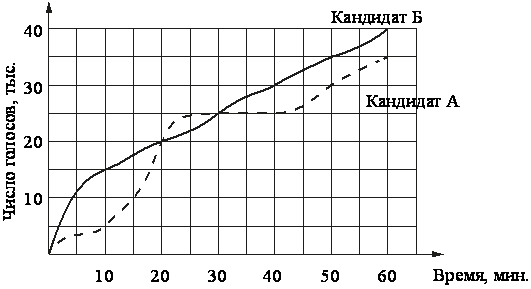 На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 30 минут дебатов?
На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 30 минут дебатов?
Комментарии: