Решение какого из данных неравенств изображено на рисунке?
1) x2-6x<0
2) x2-6x>0
3) x2-36<0
4) x2-36>0
Посмотрим на предложенные неравенства:
- все они квадратичные, т.е. графики этих функций - параболы
- у всех аргумент "а" равен еденице, т.е. больше нуля, следовательно ветви их парабол направлены вверх
- графики парабол 1) и 2) будут совпадать, т.к. это одинаковые функции.
- графики парабол 3) и 4) будут совпадать, т.к. это одинаковые функции.
Посмотрим на рисунок решения неравенства:
- корни квадратичной функции должны быть 0 и 6.
Решим уравнение x2-6x=0
x(x-6)=0
Произведение равно нулю, когда один из множителей равен нулю, получаем:
x1=0
x-6=0 => x2=6
Значит неравенства 1) и 2) подходят (судя по корням).
Проверим x2-36=0
x2-62=0
(x-6)(x+6)=0
x-6=0 => x1=6
x+6=0 => x2=-6
Неравенства 3) и 4) не подходят.
Посмотрим на рисунок, в условии показаны диапазоны, когда график функции выше оси Х, т.е. больше нуля, следовательно, подходит неравенство x2-6x>0
Ответ: 2)
Поделитесь решением
Присоединяйтесь к нам...
Расстояние между двумя пристанями по реке равно 24 км. Моторная лодка прошла от одной пристани до другой, сделала стоянку на 1 ч 40 мин и вернулась обратно. Всё путешествие заняло 6 целых и 2/3 ч. Найдите скорость течения реки, если известно, что скорость моторной лодки в стоячей воде равна 10 км/ч.
Решите неравенство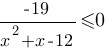 
Укажите решение неравенства
2x-x2≤0
1) (-∞;0]∪[2;+∞)
2) [0;+∞)
3) [2;+∞)
4) [0;2]
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв. м, а купить краску можно в одном из двух ближайших магазинов. Цены и характеристики краски даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,6 кг/кв. м | 5 кг | 2400 руб. | 400 руб. |
| 2 | 0,4 кг/кв. м | 4 кг | 2300 руб. | 600 руб. |
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: