
Постройте график функции y=|x|(x+1)-6x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
 y=x(x+1)-6x, при x≥0
y=x(x+1)-6x, при x≥0
y=(-x)(x+1)-6x, при x<0
 y=x2+x-6x, при x≥0
y=x2+x-6x, при x≥0
y=-x2-x-6x, при x<0
 y=x2-5x, при x≥0
y=x2-5x, при x≥0
y=-x2-7x, при x<0
Рассмотрим и построим график для каждой подфункции и объединим их.
1) y=x2-5x, при x≥0
Графиком данной подфункции является парабола. Ветви этой параболы направлены вверх, так как коэффициент при x2 положительный.
Найдем корни уравнения x2-5x=0
x(x-5)=0
x1=0
x-5=0
x2=5
Построим график по точкам:
| X | 0 | 1 | 5 | 6 |
| Y | 0 | -4 | 0 | 6 |
| X | 0 | -1 | -7 | -8 |
| Y | 0 | 6 | 0 | -8 |
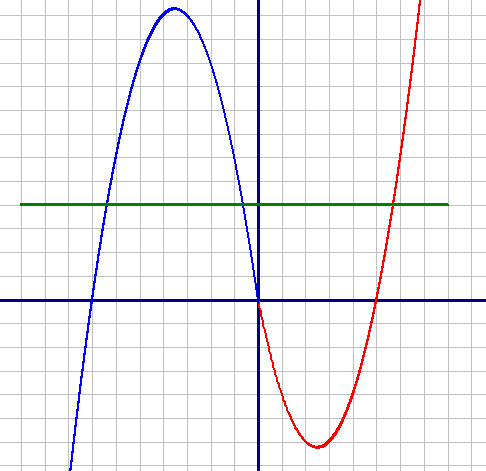 Красный график: y=x2-5x, при x≥0
Красный график: y=x2-5x, при x≥0Поделитесь решением
Присоединяйтесь к нам...
На рисунках изображены графики функций вида y=ax2+bx+c. Установите соответствие между знаками коэффициентов a и c и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, c<0
Б) a>0, c>0
В) a<0, c>0
ГРАФИКИ
1)  2)
2)  3)
3) 
В таблице под каждой буквой укажите соответствующий номер.
 На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику,
через сколько минут с момента запуска двигатель нагреется до 40°C.
На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия. Определите по графику,
через сколько минут с момента запуска двигатель нагреется до 40°C.
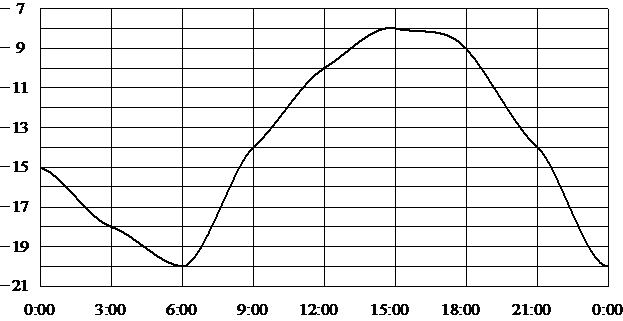 На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры во второй половине суток. Ответ дайте в градусах Цельсия.
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры во второй половине суток. Ответ дайте в градусах Цельсия.
Постройте график функции 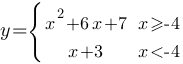 и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции
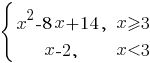
Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Комментарии:
(2015-05-25 17:31:46) Александра: Спасибо вам! Отличный сайт!
(2015-05-13 23:07:27) : Спасибо!