
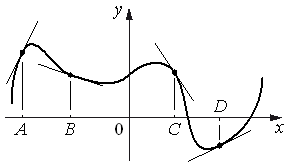
 На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| A | 1) -1,5 |
| B | 2) 0,5 |
| C | 3) 2 |
| D | 4) -0,3 |
Производную от функции, в данном случае, лучше рассматривать как тангенс угла наклона касательной.
Если тангенс положительный (т.е. угол острый), то и производная положительна и наоборот.
Тогда сразу можно сказать, что в точках A и D - значение производной положительно.
А в точках B и C - отрицательно.
Если посмотреть на таблицу углов, то ставится понятно, что при увеличени угла значение тангенса увеличивается (tg0°=0, tg45°=1, tg90°=+∞).
Следовательно, значение тангенса в точке A больше значения тангенса в точке D.
Получаем, что:
В точке A - значение производной равно 2.
В точке D - значение производной равно 0,5.
При дальнейшем увеличении угла (от 90° до 180°) значение тангенса меняется от -∞ до 0, т.е. уменьшается.
Следовательно, в точке B значение производной равно -0,3, а в точке C - значение производной равно -1,5.
Ответ:
| A | B | C | D |
| 3) | 4) | 1) | 2) |
Поделитесь решением
Присоединяйтесь к нам...
На графике изображена зависимость частоты пульса гимнаста от времени
в течение и после его выступления в вольных упражнениях.
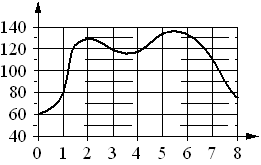
На горизонтальной оси отмечено время (в минутах), прошедшее с начала выступления гимнаста, на вертикальной оси — частота пульса (в ударах в минуту).
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику пульса гимнаста на этом интервале.
| ИНТЕРВАЛЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 4-5 мин. | 1) частота пульса упала до 110 уд./мин. |
| Б) 5-6 мин. | 2) частота пульса упала ниже 80 уд./мин. |
| В) 6-7 мин. | 3) частота пульса достигла максимума за всё время выступления и после него |
| Г) 7-8 мин. | 4) частота пульса росла на всём интервале |
На рисунке точками показаны объёмы месячных продаж обогревателей
в магазине бытовой техники. По горизонтали указываются месяцы,
по вертикали — количество проданных обогревателей. Для наглядности точки соединены линией.
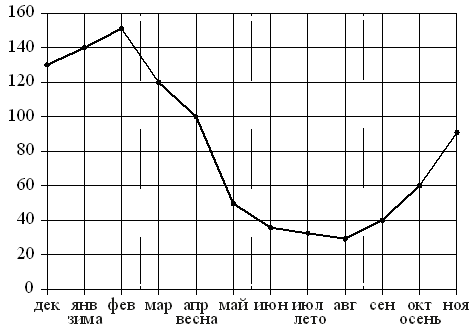
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей.
| ПЕРИОДЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) зима | 1) ежемесячный объём продаж был меньше 40 штук в течение всего периода |
| Б) весна | 2) падение объёма продаж более чем на 60 штук за период |
| В) лето | 3) ежемесячный объём продаж достиг максимума |
| Г) осень | 4) ежемесячный объём продаж рос, но был меньше 100 штук |
В таблице показано расписание пригородных электропоездов по направлению Москва Ленинградская – Клин – Тверь.
| Номер электрички |
Москва Ленинградская |
Клин | Тверь |
| 1 | 17:31 | 19:04 | |
| 2 | 17:46 | 19:08 | 19:55 |
| 3 | 18:10 | 19:28 | 20:15 |
| 4 | 18:15 | 19:37 | 21:11 |
| 5 | 18:21 | 19:50 | |
| 6 | 19:14 | 20:55 | |
| 7 | 19:21 | 21:10 | 22:11 |
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ФУНКЦИИ
А) 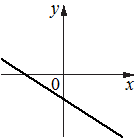 Б)
Б) 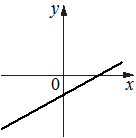 В)
В) 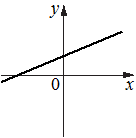 Г)
Г) 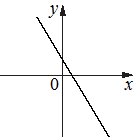
КОЭФФИЦИЕНТЫ
1) k<0, b<0
2) k>0, b>0
3) k>0, b<0
4) k<0, b>0
В таблице под каждой буквой укажите соответствующий номер.
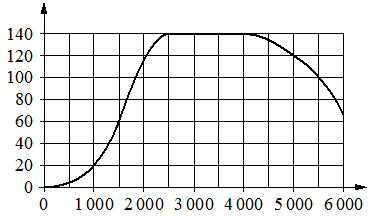 На графике показана зависимость крутящего момента автомобильного двигателя от числа оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси — крутящий момент в Н?м. Чтобы автомобиль начал движение, крутящий момент должен быть не менее 20 Н*м.
На графике показана зависимость крутящего момента автомобильного двигателя от числа оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси — крутящий момент в Н?м. Чтобы автомобиль начал движение, крутящий момент должен быть не менее 20 Н*м.
Определите по графику, какого наименьшего числа оборотов двигателя в минуту достаточно, чтобы автомобиль начал движение.
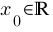 определена функция
определена функция 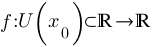 . Производной функции ƒ в точке x0 называется предел, если он существует,
. Производной функции ƒ в точке x0 называется предел, если он существует, 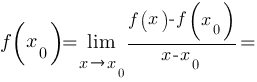
 .
.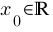 определена функция
определена функция 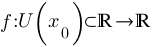 . Производной функции называется такое число A, что функцию в окрестности U(x0) можно представить в виде ƒ(x0+h)=ƒ(x0)+Ah+o(h), если A существует.
. Производной функции называется такое число A, что функцию в окрестности U(x0) можно представить в виде ƒ(x0+h)=ƒ(x0)+Ah+o(h), если A существует.
Комментарии: