Геометрическая прогрессия задана условием bn=160*(3)n. Найдите сумму первых её 7 членов.
Чтобы найти сумму первых 7 членов данной
геометрической прогрессии, воспользуемся
формулами. В нашем случае, удобней воспользоваться первой. Для этого необходимо узнать b1 - первый член прогрессии и q -
знаменатель прогрессии.
b1=160*31=480 (из условия задачи). А q=3.
Тогда S7=480*(1-37)/(1-3)=480*(1-2187)/(-2)=480*(-2186)/(-2)=524640
Ответ: S7=524640
Поделитесь решением
Присоединяйтесь к нам...
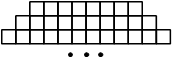Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 2 квадрата больше, чем в предыдущей. Сколько квадратов в 117-й строке?
Дана арифметическая прогрессия: 4; 7; 10; … . Найдите сумму первых шестидесяти пяти её членов.
Выписаны первые несколько членов арифметической прогрессии: -6; -3; 0; … Найдите сумму первых десяти её членов.
Дана арифметическая прогрессия (an), для которой a6=-7,8, a19=-10,4. Найдите разность прогрессии.
Дана арифметическая прогрессия: 6; 10; 14; … . Найдите сумму первых пятидесяти её членов.
Хочу получать новые решения
Ни какого спама
Автор: Таська
,
Комментарии:
(2016-02-28 15:01:10) Администратор: Фарит, я не могу посмотреть файл на вашем компьютере, поэтому я не вижу формулу...
(2016-02-28 11:59:35) фарит: почему мы не пользовались той формулой которую дают перед экзаменом? file:///C:/Users/User/YandexDisk-schackurov.farit/Скриншоты/2016-02-28%2011-56-59%20Скриншот%20экрана.png