
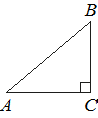
 В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.
В треугольнике ABC угол C равен 90°, AB=25, AC=24. Найдите cosB.
По определению:
cosB=BC/AB
Чтобы найти BC можно использовать
теорему Пифагора:
AB2=BC2+AC2
252=BC2+242
625=BC2+576
BC2=49
BC=7
Теперь можем найти косинус:
cosB=BC/AB=7/25=0,28
Ответ: 0,28
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь ромба, если его высота равна 6, а острый угол равен 30°.
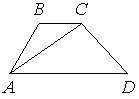 В трапеции ABCD известно, что AD=8, BC=7, а её площадь равна 45. Найдите площадь треугольника ABC.
В трапеции ABCD известно, что AD=8, BC=7, а её площадь равна 45. Найдите площадь треугольника ABC.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
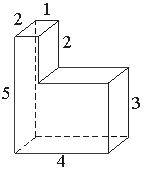 Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
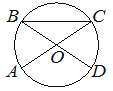 В окружности с центром O отрезки AC и BD — диаметры. Вписанный угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах.
В окружности с центром O отрезки AC и BD — диаметры. Вписанный угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах.

Комментарии: