В треугольнике ABC проведена биссектриса AL, угол ALC равен 145°, угол ABC равен 113°. Найдите угол ACB. Ответ дайте в градусах.
Пусть ∠BAL=x
Тогда, ∠LAC тоже =x (так как AL -
биссектриса).
Рассмотрим треугольник ABC:
∠ABC+∠ACB+∠CAB=180° (по
теореме о сумме углов треугольника).
113°+∠ACB+2x=180°
∠ACB+2x=67°
x=(67°-∠ACB)/2
Рассмотрим треугольник ALC:
∠ALC+∠ACB+∠LAC=180° (по
теореме о сумме углов треугольника).
145°+∠ACB+x=180°
∠ACB+x=35°
Подставляем значение x, полученное ранее:
∠ACB+(67°-∠ACB)/2=35° |*2
2∠ACB+67°-∠ACB=70°
∠ACB+67°=70°
∠ACB=70°-67°=3°
Ответ: 3
Поделитесь решением
Присоединяйтесь к нам...
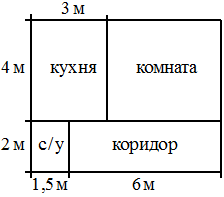Квартира состоит из комнаты, кухни, коридора и санузла (см. чертёж). Кухня имеет размеры 3м x 4м, санузел — 1,5м x 2м, длина коридора 6м. Найдите площадь комнаты (в квадратных метрах).
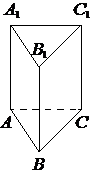Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4√3. Найдите объём призмы ABCA1B1C1.
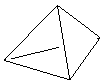Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
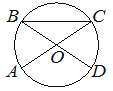В окружности с центром O отрезки AC и BD — диаметры. Вписанный угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах.
В равнобедренном треугольнике ABC боковая сторона AB=25, sinA=3/5. Найдите площадь треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: