В треугольнике ABC проведена биссектриса AL, угол ALC равен 145°, угол ABC равен 113°. Найдите угол ACB. Ответ дайте в градусах.
Пусть ∠BAL=x
Тогда, ∠LAC тоже =x (так как AL -
биссектриса).
Рассмотрим треугольник ABC:
∠ABC+∠ACB+∠CAB=180° (по
теореме о сумме углов треугольника).
113°+∠ACB+2x=180°
∠ACB+2x=67°
x=(67°-∠ACB)/2
Рассмотрим треугольник ALC:
∠ALC+∠ACB+∠LAC=180° (по
теореме о сумме углов треугольника).
145°+∠ACB+x=180°
∠ACB+x=35°
Подставляем значение x, полученное ранее:
∠ACB+(67°-∠ACB)/2=35° |*2
2∠ACB+67°-∠ACB=70°
∠ACB+67°=70°
∠ACB=70°-67°=3°
Ответ: 3
Поделитесь решением
Присоединяйтесь к нам...
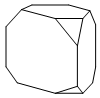От деревянной правильной треугольной призмы отпилили все её вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
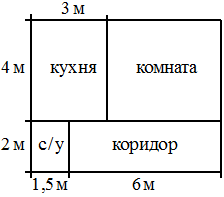Квартира состоит из комнаты, кухни, коридора и санузла (см. чертёж). Кухня имеет размеры 3м x 4м, санузел — 1,5м x 2м, длина коридора 6м. Найдите площадь комнаты (в квадратных метрах).
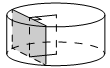Радиус основания цилиндра равен 15, а его образующая
равна 14. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
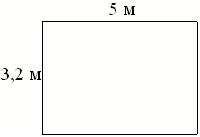На плане указано, что прямоугольная комната имеет площадь 15,7 кв. м. Точные измерения показали, что ширина комнаты равна 3,2 м, а длина 5 м.
На сколько квадратных метров площадь комнаты отличается от значения, указанного на плане?
Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: