
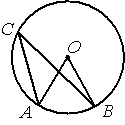
 Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию ∠AOB=84°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 84°. ∠ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 84/2=42.
Ответ: 42
Поделитесь решением
Присоединяйтесь к нам...
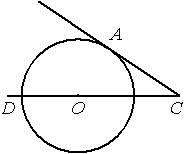 Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
100°.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
100°.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Комментарии:
(2015-05-16 09:34:37) LBVF: SPS
(2015-04-03 20:28:39) БАТРАДЗ: спс разобрался