
Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его медианой.
2) Диагонали прямоугольника равны.
3) У любой трапеции боковые стороны равны.
Рассмотрим каждое утверждение:
1) "Каждая из
биссектрис равнобедренного треугольника является его
медианой." Это утверждение неверно,
т.к. противоречит свойствам равнобедренного треугольника.
Только
биссектриса, проведенная к основанию является и
медианой и
высотой.
2) "Диагонали прямоугольника равны." Это утверждение верно
по свойству прямоугольника.
3) "У любой трапеции боковые стороны равны", это утверждение неверно, боковые стороны равны только у
равнобедренной трапеции.
Поделитесь решением
Присоединяйтесь к нам...
 Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.
Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.
 В трапеции ABCD основания AD и BC равны соответственно 33 и 11,
а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
В трапеции ABCD основания AD и BC равны соответственно 33 и 11,
а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
 Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 57.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 57.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
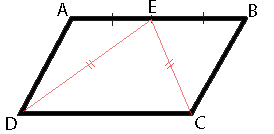 В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
Комментарии:
(2017-01-27 21:13:41) Администратор: Лиля, посмотрите задачу 293 в разделе "Числа и вычисления", похожа на Вашу.
(2017-01-27 19:22:55) лиля: Нож каторый стоит 120рублей,прадается с 15-процентной скидкой.При покупки6таких ножей покупатель отдал кассира 1000рублей.Сколько рублей он должен получить