
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ17 –ł–∑ 287 |
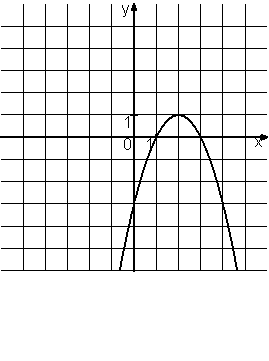 –Ě–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–į —Ą—É–Ĺ–ļ—Ü–ł—Ź –≤–ł–ī–į y=ax2+bx+c. –£—Ā—ā–į–Ĺ–ĺ–≤–ł—ā–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ľ–Ķ–∂–ī—É —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—Ź–ľ–ł –ł –Ņ—Ä–ĺ–ľ–Ķ–∂—É—ā–ļ–į–ľ–ł, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä—č—Ö —ć—ā–ł —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—Ź —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—ā—Ā—Ź.
–Ě–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–į —Ą—É–Ĺ–ļ—Ü–ł—Ź –≤–ł–ī–į y=ax2+bx+c. –£—Ā—ā–į–Ĺ–ĺ–≤–ł—ā–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ľ–Ķ–∂–ī—É —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—Ź–ľ–ł –ł –Ņ—Ä–ĺ–ľ–Ķ–∂—É—ā–ļ–į–ľ–ł, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä—č—Ö —ć—ā–ł —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—Ź —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—ā—Ā—Ź.
–£–Ę–í–ē–†–Ė–Ē–ē–Ě–ė–Į
–ź) –§—É–Ĺ–ļ—Ü–ł—Ź –≤–ĺ–∑—Ä–į—Ā—ā–į–Ķ—ā –Ĺ–į –Ņ—Ä–ĺ–ľ–Ķ–∂—É—ā–ļ–Ķ
–Ď) –§—É–Ĺ–ļ—Ü–ł—Ź —É–Ī—č–≤–į–Ķ—ā –Ĺ–į –Ņ—Ä–ĺ–ľ–Ķ–∂—É—ā–ļ–Ķ
–ü–†–ě–ú–ē–Ė–£–Ę–ö–ė
1) [0;3]
2) [-1;1]
3) [2;4]
4) [1;4]
 –í–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł–Ķ –ł–Ľ–ł —É–Ī—č–≤–į–Ĺ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ–ľ —Ą—É–Ĺ–ļ—Ü–ł–ł –Ņ—Ä–ł "–ī–≤–ł–∂–Ķ–Ĺ–ł–ł" –Ņ–ĺ –ĺ—Ā–ł —Ö —Ā–Ľ–Ķ–≤–į –Ĺ–į–Ņ—Ä–į–≤–ĺ. –ē—Ā–Ľ–ł –ļ–į–∂–ī–ĺ–Ķ –Ņ–ĺ—Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –Ī–ĺ–Ľ—Ć—ą–Ķ –Ņ—Ä–Ķ–ī—č–ī—É—Č–Ķ–≥–ĺ, —ā–ĺ —Ą—É–Ĺ–ļ—Ü–ł—Ź –≤–ĺ–∑—Ä–į—Ā—ā–į–Ķ—ā, –Ķ—Ā–Ľ–ł –ľ–Ķ–Ĺ—Ć—ą–Ķ - —É–Ī—č–≤–į–Ķ—ā.
–í–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł–Ķ –ł–Ľ–ł —É–Ī—č–≤–į–Ĺ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ–ľ —Ą—É–Ĺ–ļ—Ü–ł–ł –Ņ—Ä–ł "–ī–≤–ł–∂–Ķ–Ĺ–ł–ł" –Ņ–ĺ –ĺ—Ā–ł —Ö —Ā–Ľ–Ķ–≤–į –Ĺ–į–Ņ—Ä–į–≤–ĺ. –ē—Ā–Ľ–ł –ļ–į–∂–ī–ĺ–Ķ –Ņ–ĺ—Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –Ī–ĺ–Ľ—Ć—ą–Ķ –Ņ—Ä–Ķ–ī—č–ī—É—Č–Ķ–≥–ĺ, —ā–ĺ —Ą—É–Ĺ–ļ—Ü–ł—Ź –≤–ĺ–∑—Ä–į—Ā—ā–į–Ķ—ā, –Ķ—Ā–Ľ–ł –ľ–Ķ–Ĺ—Ć—ą–Ķ - —É–Ī—č–≤–į–Ķ—ā.
–ź) –§—É–Ĺ–ļ—Ü–ł—Ź –≤–ĺ–∑—Ä–į—Ā—ā–į–Ķ—ā –Ĺ–į –Ņ—Ä–ĺ–ľ–Ķ–∂—É—ā–ļ–Ķ (-∞;2], —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –ł–∑ –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—č—Ö –Ņ–ĺ–ī—Ö–ĺ–ī–ł—ā —ā–ĺ–Ľ—Ć–ļ–ĺ –Ņ—Ä–ĺ–ľ–Ķ–∂—É—ā–ĺ–ļ [-1;1]
–Ď) –§—É–Ĺ–ļ—Ü–ł—Ź —É–Ī—č–≤–į–Ķ—ā –Ĺ–į –Ņ—Ä–ĺ–ľ–Ķ–∂—É—ā–ļ–Ķ (2;+∞), —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ł–∑ –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—č—Ö –Ņ–ĺ–ī—Ö–ĺ–ī–ł—ā –Ņ—Ä–ĺ–ľ–Ķ–∂—É—ā–ĺ–ļ [2;4]
–ě—ā–≤–Ķ—ā: A) - 2); –Ď) - 3)
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
–£—Ā—ā–į–Ĺ–ĺ–≤–ł—ā–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ľ–Ķ–∂–ī—É –≥—Ä–į—Ą–ł–ļ–į–ľ–ł —Ą—É–Ĺ–ļ—Ü–ł–Ļ –ł —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ–ł, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ł—Ö –∑–į–ī–į—é—ā.
| –§–ě–†–ú–£–õ–ę | –ď–†–ź–§–ė–ö–ė | ||
|
1) y=-3 2) y=x-3 3) y=-3x 4) y=3x |
–ź) 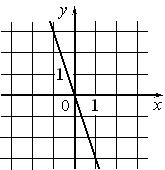 |
–Ď)  |
–í)  |
–ü–ĺ—Ā—ā—Ä–ĺ–Ļ—ā–Ķ –≥—Ä–į—Ą–ł–ļ —Ą—É–Ĺ–ļ—Ü–ł–ł 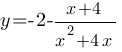 –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ, –Ņ—Ä–ł –ļ–į–ļ–ł—Ö –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź—Ö m –Ņ—Ä—Ź–ľ–į—Ź y=m –Ĺ–Ķ –ł–ľ–Ķ–Ķ—ā —Ā –≥—Ä–į—Ą–ł–ļ–ĺ–ľ –ĺ–Ī—Č–ł—Ö —ā–ĺ—á–Ķ–ļ.
–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ, –Ņ—Ä–ł –ļ–į–ļ–ł—Ö –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź—Ö m –Ņ—Ä—Ź–ľ–į—Ź y=m –Ĺ–Ķ –ł–ľ–Ķ–Ķ—ā —Ā –≥—Ä–į—Ą–ł–ļ–ĺ–ľ –ĺ–Ī—Č–ł—Ö —ā–ĺ—á–Ķ–ļ.
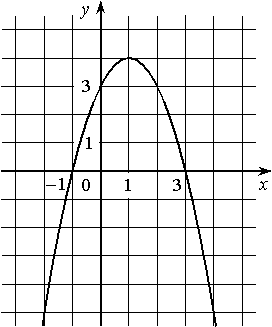 –Ě–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ –≥—Ä–į—Ą–ł–ļ –ļ–≤–į–ī—Ä–į—ā–ł—á–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł y=f(x).
–Ě–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ –ł–∑–ĺ–Ī—Ä–į–∂—Ď–Ĺ –≥—Ä–į—Ą–ł–ļ –ļ–≤–į–ī—Ä–į—ā–ł—á–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł y=f(x).
–ö–į–ļ–ł–Ķ –ł–∑ —Ā–Ľ–Ķ–ī—É—é—Č–ł—Ö —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ļ –ĺ –ī–į–Ĺ–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≤–Ķ—Ä–Ĺ—č–ľ–ł? –ó–į–Ņ–ł—ą–ł—ā–Ķ –ł—Ö –Ĺ–ĺ–ľ–Ķ—Ä–į.
1) f(x)<0 –Ņ—Ä–ł x<1
2) –Ě–į–ł–Ī–ĺ–Ľ—Ć—ą–Ķ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł —Ä–į–≤–Ĺ–ĺ 4
3) –§—É–Ĺ–ļ—Ü–ł—Ź –≤–ĺ–∑—Ä–į—Ā—ā–į–Ķ—ā –Ĺ–į –Ņ—Ä–ĺ–ľ–Ķ–∂—É—ā–ļ–Ķ (-∞; 1]
–£—Ā—ā–į–Ĺ–ĺ–≤–ł—ā–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ľ–Ķ–∂–ī—É –≥—Ä–į—Ą–ł–ļ–į–ľ–ł —Ą—É–Ĺ–ļ—Ü–ł–Ļ –ł —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ–ł, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ł—Ö –∑–į–ī–į—é—ā.
–ď–†–ź–§–ė–ö–ė
A) 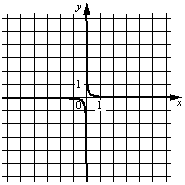 –Ď)
–Ď) 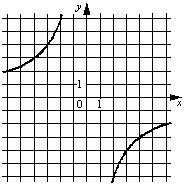 –í)
–í) 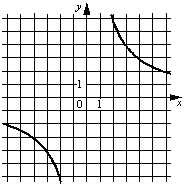
–§–ě–†–ú–£–õ–ę
1) y=12/x
2) y=-12/x
3) y=1/(12x)
–í —ā–į–Ī–Ľ–ł—Ü–Ķ –Ņ–ĺ–ī –ļ–į–∂–ī–ĺ–Ļ –Ī—É–ļ–≤–ĺ–Ļ —É–ļ–į–∂–ł—ā–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ļ –Ĺ–ĺ–ľ–Ķ—Ä.
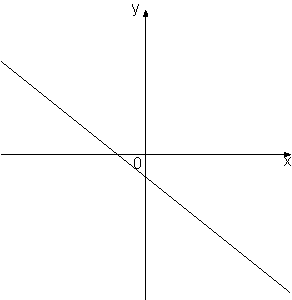
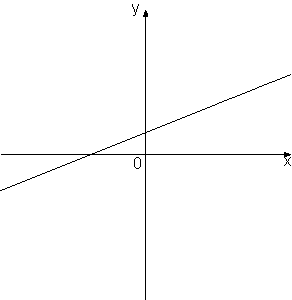
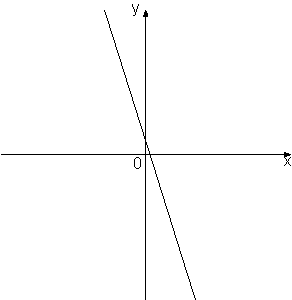
–Ě–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ—č –≥—Ä–į—Ą–ł–ļ–ł —Ą—É–Ĺ–ļ—Ü–ł–Ļ –≤–ł–ī–į
y=kx+b. –£—Ā—ā–į–Ĺ–ĺ–≤–ł—ā–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–Ķ –ľ–Ķ–∂–ī—É –∑–Ĺ–į–ļ–į–ľ–ł –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ĺ–≤ k –ł b –ł –≥—Ä–į—Ą–ł–ļ–į–ľ–ł.
–ö–ě–≠–§–§–ė–¶–ė–ē–Ě–Ę–ę
–ź) k<0, b<0
–Ď) k>0, b>0
–í) k<0, b>0
1)
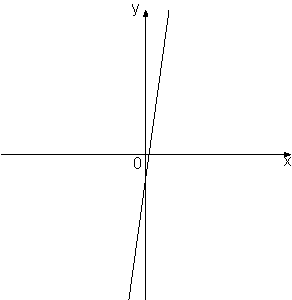
2)
3)
4)
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: