
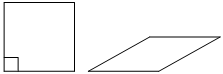
 Ромб и квадрат имеют равные стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 16.
Ромб и квадрат имеют равные стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 16.
Площадь квадрата равна квадрату его стороны:
Sкв=a2=16
a=4
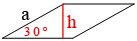 Площадь ромба равна произведению основания на высоту:
Площадь ромба равна произведению основания на высоту:
Sр=a*h
sin30°=h/a (по определению)
1/2=h/4
h=1*4/2=2
Sр=a*h=4*2=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
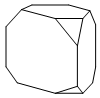 От деревянной правильной треугольной призмы отпилили все её вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
От деревянной правильной треугольной призмы отпилили все её вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
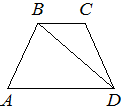 В трапеции ABCD известно, что AB=CD, ∠BDA=40° и ∠BDC=30°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD известно, что AB=CD, ∠BDA=40° и ∠BDC=30°. Найдите угол ABD. Ответ дайте в градусах.
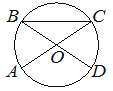 В окружности с центром O отрезки AC и BD — диаметры. Вписанный угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах.
В окружности с центром O отрезки AC и BD — диаметры. Вписанный угол ACB равен 36°. Найдите угол AOD. Ответ дайте в градусах.
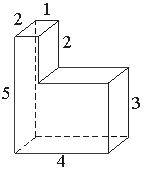 Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
 Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа
на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Комментарии: