
Задача №17 из 42 |
Решите уравнение x2=16.
Если уравнение имеет более одного корня, в ответе укажите больший из них.
x2=16
x2-16=0
Можно решить это квадратное уравнение через дискриминант, но легче решить, используя формулу
разность квадратов:
x2-42=0
(x-4)(x+4)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x-4=0 => x1=4
2) x+4=0 => x1=-4
Наибольший корень - это x1=4
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
Найдите корень уравнения 9x+2(1-6x)=-x-6.
Некоторые учащиеся 11-х классов школы ходили в октябре на спектакль «Вишнёвый сад». В декабре некоторые одиннадцатиклассники пойдут
на постановку по пьесе «Три сестры», причём среди них не будет тех, кто ходил в октябре на спектакль «Вишнёвый сад».
Выберите утверждения, которые будут верны при указанных условиях независимо от того, кто из одиннадцатиклассников пойдёт на постановку по пьесе «Три сестры».
1) Нет ни одного одиннадцатиклассника, который ходил на спектакль «Вишнёвый сад» и пойдёт на постановку по пьесе «Три сестры».
2) Каждый учащийся 11-х классов, который не был на спектакле «Вишнёвый сад», пойдёт на постановку по пьесе «Три сестры».
3) Среди учащихся 11-х классов этой школы, которые не пойдут на постановку по пьесе «Три сестры», есть хотя бы один, который ходил на спектакль «Вишнёвый сад».
4) Найдётся одиннадцатиклассник, который не ходил на спектакль «Вишнёвый сад» и не пойдёт на постановку по пьесе «Три сестры».
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Найдите корень уравнения 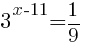
Найдите корень уравнения √
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок, делая первый прыжок из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, совершив ровно 8 прыжков?
Комментарии: