
 На рисунке изображён график квадратичной функции y=f(x).
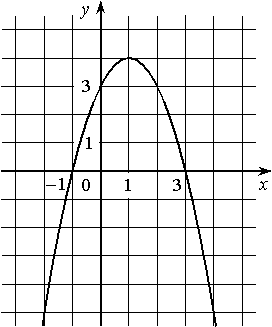
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) f(x)<0 при x<1
2) Наибольшее значение функции равно 4
3) Функция возрастает на промежутке (-∞; 1]
Рассмотрим каждое утверждение:
1) f(x)<0 при x<1, это утверждение неверно, так как, на промежутке (-1; 1) график функции располагается выше оси Х, т.е. f(x)>0. Например, видно что f(0)=3.
2) Наибольшее значение функции равно 4. Это утверждение верно, так как из графика видно, что f(1)=4 и эта точка - вершина параболы.
3) Функция возрастает на промежутке (-∞; 1]. Функция возрастает, если выполняется условие:
x1>x2, то и f(x1)>f(x2).
Посмотрим на наш график:
-1<0 - очевидно
f(-1)=0
f(0)=3
Т.е. f(-1)<f(0) - условие выполняется. И оно будет выполняться для всех х на промежутке (-∞; 1], т.о. данное утверждение верно.
Ответ: 2) и 3)
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции:
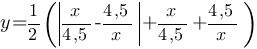 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
A) 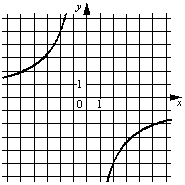 Б)
Б) 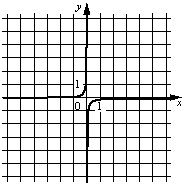 В)
В) 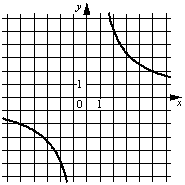
ФОРМУЛЫ
1) y=-10/x
2) y=-1/(10x)
3) y=10/x
В таблице под каждой буквой укажите соответствующий номер.
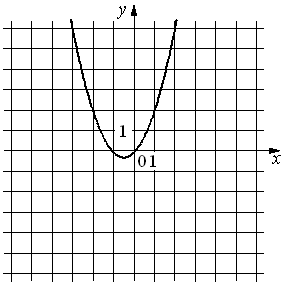 На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
На рисунке изображён график функции y=ax2+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
| УТВЕРЖДЕНИЯ | ПРОМЕЖУТКИ |
| А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
1) [-3;3] 2) [0;3] 3) [-3;-1] 4) [-3;0] |
Постройте график функции 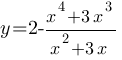 и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
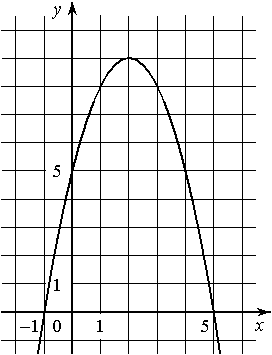 На рисунке изображён график квадратичной функции y=ƒ(x).
На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке [2;+∞)
2) ƒ(x)>0 при -1<x<5
3) ƒ(0)<ƒ(4)
Комментарии: