На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) a<0, c>0 2) a>0, c>0 3) a>0, c<0 4) a<0, c<0 |
А)  |
Б)  |
В)  |
Рассмотрим каждый график:
А) Ветви параболы направлены вверх, значит коэффициент а>0. Если х приравнять к нулю, то получим y=a*02+b*0+c, т.е. y=c.
На данном графике при x=0, y - отрицательный, следовательно и c<0.
Таким образом получаем, что данному графику соответствует ответ 3)
Б) Ветви параболы направлены вверх, значит a>0. При x=0, y - положительный, следовательно и c>0.
Соответствует ответу 2)
В) Ветви параболы направлены вниз, значит a<0. При x=0, y - положительный, следовательно и c>0.
Соответствует ответу 1)
Ответ: А) - 3), Б) - 2, В) - 1)
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции y=|x|x+3|x|-5x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции y=(x2+6,25)(x-1)/(1-x) и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Постройте график функции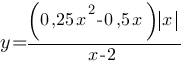 
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=-3 2) y=x-3 3) y=-3x 4) y=3x |
А)  |
Б)  |
В)  |
Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=x2+6,25 ровно одну общую точку. Постройте этот график и все такие прямые.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: