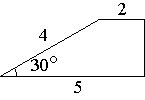
Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 2 и 5.
Площадь
трапеции вычисляется по формуле 
, где a и b - основания трапеции,
а h - высота трапеции. Обозначим углы трапеции A, B, C и D. И проведем высоту из угла B к основанию AD, как паказано на рисунке.
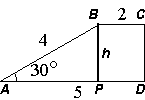Получившийся треугольник ABP -
прямоугольный c катетами BP и AP. Заметим, что BP - это катет притиволежащий углу в 30°, следовательно он равен половине
гипотенузы (
по свойству прямоугольного треугольника), h=4/2=2. Используя формулу площади трапеции получаем S=(2+5)*2/2.
Вычисляем S=7.
Ответ: S=7.
Поделитесь решением
Присоединяйтесь к нам...
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
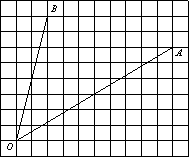Найдите тангенс угла AOB.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-25 18:11:21) Lina: Огромное спасибо
(2015-05-21 18:06:36) Динар: Спасибо
(2015-05-16 09:40:34) : SPS
(2015-03-21 16:07:42) Анна: замечательно!!!!